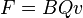Magnetic field
From Wikipedia, the free encyclopedia
| This article may require cleanup to meet Wikipedia's quality standards. Please discuss this issue on the talk page or replace this tag with a more specific message. This article has been tagged since May 2007. |
| Electromagnetism | |
| Electricity · Magnetism | |
| Electrostatics | |
|---|---|
| Electric charge | |
| Coulomb's law | |
| Electric field | |
| Gauss's law | |
| Electric potential | |
| Electric dipole moment | |
| Magnetostatics | |
| Ampère's circuital law | |
| Magnetic field | |
| Magnetic flux | |
| Biot-Savart law | |
| Magnetic dipole moment | |
| Electrodynamics | |
| Electrical current | |
| Lorentz force law | |
| Electromotive force | |
| (EM) Electromagnetic induction | |
| Faraday-Lenz law | |
| Displacement current | |
| Maxwell's equations | |
| (EMF) Electromagnetic field | |
| (EM) Electromagnetic radiation | |
| Electrical Network | |
| Electrical conduction | |
| Electrical resistance | |
| Capacitance | |
| Inductance | |
| Impedance | |
| Resonant cavities | |
| Waveguides | |
| Tensors in Relativity | |
| Electromagnetic tensor | |
| Electromagnetic stress-energy tensor | |
In physics, the space surrounding moving electric charges, changing electric fields and magnetic dipoles contains a magnetic field. Other moving charges and magnetic dipoles in this space experience a force. Magnets are one common example of a magnetic dipole.
The field is technically referred to as a solenoidal vector field. The direction of a magnetic field can be demonstrated with magnetic dipoles; magnetic dipoles in a magnetic field align themselves to be parallel with the field lines, as can be seen when iron filings are in the presence of a magnet. Unlike the electric field, the force exerted by a magnetic field does no work (Physics). Magnetic fields also have an energy density proportional to the square of the field intensity. The magnetic field is measured in the SI units of teslas.
There are some notable specific incarnations of the magnetic field. For the physics of magnetic materials, see magnetism, and more specifically ferromagnetism, paramagnetism, and diamagnetism. For constant magnetic fields, such as dipoles and currents, see magnetostatics. For magnetic fields created by changing electric fields, see electromagnetism.
The electric field and the magnetic field are considered fundamentally the same field, known as the electromagnetic field.
Contents
|
[edit] Definition
The magnetic field 
is a vector field (that is, some vector at every point of space and time), with SI units of Tesla (one Tesla is one newton-second per coulomb-metre). The field can be defined in several different but physically equivilent ways.
The simplest definition to state is that the magnetic field (along with the electric field) is the solution to Maxwell's Equations. For example, as a special case of this, the magnetic field of a point charge moving at constant velocity, as first derived by Oliver Heaviside[1], is (in SI units):
where
is velocity vector of the electric charge,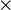
indicates a vector cross product,
is the speed of light in a vacuum,- and
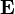is the electric field vector.
An alternate (but physically equivalent) definition of the magnetic field is that a charged particle moving through a magnetic field undergoes a magnetic force related to the charge and velocity by the Lorentz force law (see below), which in SI units states:
where
is the magnetic force (a vector),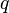
is particle's electric charge,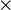- again indicates a vector cross product,
- and
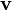is particle's velocity vector.
By moving a test charge through a region of space, and measuring the dependence of force on velocity, one can work backwards using this equation to measure the magnetic field.
It follows from either definition that the magnetic field vector (being a vector product) is a pseudovector (also called an axial vector).
Intuitively can be seen as a vector whose direction gives the axis of the possible directions of the force on a charged particle due to the magnetic field; the possible directions being at right angles to the axis , and the exact direction being at right angles to both the velocity of the particle and . The magnitude of is the amount of force the magnetic field causes on the particle, per unit of particle charge by particle speed.
Another intuitive way to view is as a bundle of lines of force that pull two unlike magnetic poles together; this view is particularly appropriate in the context of magnetic dipoles (also see below).
[edit] B and H
There are two quantities that physicists may refer to as the magnetic field, notated 
and . The vector field is known among electrical engineers as the magnetic field intensity or magnetic field strength also known as auxiliary magnetic field. The vector field is known as magnetic flux density or magnetic induction or simply magnetic field, as used by physicists, and has the SI units of Tesla (T), equivalent to webers (Wb) per square metre or volt second per square metre. Magnetic flux has the SI units of webers so the field is that of its density (an areal density). [1][2][3][4][2] The vector field has the SI units of amperes per metre and is something of the magnetic analog to the electric displacement field represented by 
, with the SI units of the latter being ampere-seconds per square metre. Although the term "magnetic field" was historically reserved for , with being termed the "magnetic induction", is now understood to be the more fundamental entity, and most modern writers refer to as the magnetic field, except when context fails to make it clear whether the quantity being discussed is or . See: [3]
The difference between the and the vectors can be traced back to Maxwell's 1855 paper entitled On Faraday's Lines of Force. It is later clarified in his concept of a sea of molecular vortices that appears in his 1861 paper On Physical Lines of Force - 1861. Within that context, represented pure vorticity (spin), whereas was a weighted vorticity that was weighted for the density of the vortex sea. Maxwell considered magnetic permeability µ to be a measure of the density of the vortex sea. Hence the relationship,
(1) Magnetic induction current causes a magnetic current density
was essentially a rotational analogy to the linear electric current relationship,
(2) Electric convection current
where ρ is electric charge density. was seen as a kind of magnetic current of vortices aligned in their axial planes, with being the circumferential velocity of the vortices.
The electric current equation can be viewed as a convective current of electric charge that involves linear motion. By analogy, the magnetic equation is an inductive current involving spin. There is no linear motion in the inductive current along the direction of the vector. The magnetic inductive current represents lines of force. In particular, it represents lines of inverse square law force.
The extension of the above considerations confirms that where is to , and where 
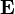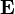is to ρ, then it necessarily follows from Gauss's law and from the equation of continuity of charge that is to . Ie. parallels with , whereas parallels with .
In SI units, 
and 
are measured in teslas (T) and amperes per metre (A/m), respectively; or, in cgs units, in gauss (G) and oersteds (Oe), respectively. Two parallel wires carrying an electric current in the same direction will generate a magnetic field that will cause a force of attraction between them. This fact is used to define the value of an ampere of electric current.
The fields and are also related by the equation
(SI units)
(cgs units),
where 
is magnetization.
[edit] Force due to a magnetic field
[edit] Force on a charged particle
where
- F is the force (in newtons)
- q is the electric charge of the particle (in coulombs)
- v is the instantaneous velocity of the particle (in meters per second)
- and × is the cross product.
[edit] Force on wire segment
Integrating the Lorentz force on an individual charged particle over a flow (current) of charged particles results in the Lorentz force on a stationary wire carrying electric current:
where
- F = forces, measured in newtons
- I = current in wire, measured in amperes
- B = magnetic field, measured in teslas
- = vector cross-product
- l = length of wire, measured in metres
In the equation above, the current vector I is a vector with magnitude equal to the scalar current, I, and direction pointing along the wire in which the current is flowing.
Alternatively, instead of current, the wire segment l can be considered a vector.
The Lorentz force on a macroscopic current carrier is often referred to as the Laplace force.
[edit] Magnetic field of a steady current
) around the wire. The field is oriented according to the right hand grip rule.The magnetic field of a steady current (a continual flow of charges, for example through a wire, which is constant in time and in which charge is neither building up nor depleting at any point), is described by the Biot-Savart law:
(in SI units), where
is a differential element of current,
is the resulting differential contribution to the magnetic field,- μ0 is the magnetic constant,
is the unit displacement vector from the current element to the field point, and- r is the distance from the current element to the field point.
This is a consequence of Ampere's law, one of the four Maxwell's equations. Alternatively, it can be thought of as a true, empirical law in its own right, which contributes to the derivation of Maxwell's equations. From a practical point of view, though, the law is true and useful regardless of its philosophical origin.
[edit] Properties
[edit] Magnetic field lines
The direction of the magnetic field vector follows from the definition above. It coincides with the direction of orientation of a magnetic dipole, such as a small magnet, or a small loop of current in the magnetic field. So, a cluster of small particles of ferromagnetic material being brought in the magnetic field can be used to show the direction of magnetic field lines (see figure). A trajectory of charged particle (electron Such motion of Solar wind plasma in the magnetic field of Earth results in Northern Lights (and Southern Lights) - spots of glow in upper atmosphere above magnetic poles of Earth where energetic electrons and protons can reach air and ionize nitrogen and oxygen molecules.
[edit] Pole labelling confusions
See also North Magnetic Pole and South Magnetic Pole.
The end of a compass needle that points north was historically called the "north" magnetic pole of the needle. Since dipoles are vectors and align "head to tail" with each other to minimize their magnetic potential energy, the magnetic pole located near the geographic North Pole is actually the "south" pole.
The "north" and "south" poles of a magnet or a magnetic dipole are labelled similarly to north and south poles of a compass needle. Near the north pole of a bar or a cylinder magnet, the magnetic field vector is directed out of the magnet; near the south pole, into the magnet. This magnetic field continues inside the magnet (so there are no actual "poles" anywhere inside or outside of a magnet where the field stops or starts). Breaking a magnet in half does not separate the poles but produces two magnets with two poles each.
Earth's magnetic field is probably produced by electric currents in its liquid core.
It can be more easily explained if one works backwards from the equation:
where
- B is the magnitude of flux density, measured in SI as teslas
- F is the force experienced by a wire, measured in Newtons
- I is the current, measured in amperes
- L is the length of the wire, measured in metres
For a magnetic flux density to equal 1 tesla, a force of 1 newton must act on a wire of length 1 metre carrying 1 ampere of current.
1 newton of force is not easily accomplished. For example: the most powerful superconducting electromagnets in the world have flux densities of 'only' 20 T. This is true obviously for both electromagnets and natural magnets, but a magnetic field can only act on moving charge — hence the current, I, in the equation.
The equation can be adjusted to incorporate moving single charges, ie protons, electrons, and so on via
where
- Q is the charge in coulombs, and
- v is the velocity of that charge in metres per second.
Fleming's left hand rule for motion, current and polarity can be used to determine the direction of any one of those from the other two, as seen in the example. It can also be remembered in the following way. The digits from the thumb to second finger indicate 'Force', 'B-field', and 'I(Current)' respectively, or F-B-I in short. For professional use, the right hand grip rule is used instead which originated from the definition of cross product in the right hand system of coordinates.
Other units of magnetic flux density are
- 1 gauss = 10-4 teslas = 100 microteslas (µT)
- 1 gamma = 10-9 teslas = 1 nanotesla (nT)
[edit] Rotating magnetic fields
The rotating magnetic field is a key principle in the operation of alternating-current motors. A permanent magnet in such a field will rotate so as to maintain its alignment with the external field. This effect was conceptualized by Nikola Tesla, and later utilised in his, and others, early AC (alternating-current) electric motors. A rotating magnetic field can be constructed using two orthogonal coils with 90 degrees phase difference in their AC currents. However, in practice such a system would be supplied through a three-wire arrangement with unequal currents. This inequality would cause serious problems in standardization of the conductor size and so, in order to overcome it, three-phase systems are used where the three currents are equal in magnitude and have 120 degrees phase difference. Three similar coils having mutual geometrical angles of 120 degrees will create the rotating magnetic field in this case. The ability of the three-phase system to create a rotating field, utilized in electric motors, is one of the main reasons why three-phase systems dominate the world's electrical power supply systems.
Because magnets degrade with time, synchronous motors and induction motors use short-circuited rotors (instead of a magnet) following the rotating magnetic field of a multicoiled stator. The short-circuited turns of the rotor develop eddy currents in the rotating field of the stator, and these currents in turn move the rotor by the Lorentz force.
In 1882, Nikola Tesla identified the concept of the rotating magnetic field. In 1885, Galileo Ferraris independently researched the concept. In 1888, Tesla gained U.S. Patent 381,968 for his work. Also in 1888, Ferraris published his research in a paper to the Royal Academy of Sciences in Turin.
[edit] Hall effect
Because the Lorentz force is charge-sign-dependent (see above), it results in charge separation when a conductor with current is placed in a transverse magnetic field, with a buildup of opposite charges on two opposite sides of conductor in the direction normal to the magnetic field, and the potential difference between these sides can be measured.
The Hall effect is often used to measure the magnitude of a magnetic field as well as to find the sign of the dominant charge carriers in semiconductors (negative electrons or positive holes).
[edit] Relativistic explanations for the magnetic field
According to special relativity, electric and magnetic forces are part of a single physical phenomenon; an electric field perceived by one observer will be perceived by another observer in a different frame of reference as a mixture of electric fields and magnetic forces. A magnetic force can be considered as simply the relativistic part of an electric field when the latter is seen by a moving observer.
There are three different arguments for this assertion. The earliest of these arguments came about in 1905 with Einstein's famous paper on the special theory of relativity. A Lorentz transformation is applied to Heaviside's versions of Maxwell's equations and this results in the appearance of the magnetic force term vXB.
In 1963, Edmund Purcell published another argument in which he applied the Lorentz-Fitzgerald contraction to a neutral current carrying wire in order to invoke an electric charge density. The principle behind Purcell's derivation was that the relativistic gamma factor combined with the induced charge was able to convert the Coulomb force into the vXB force.
More recently, textbooks on electromagnetism have been mentioning yet another relativistic approach in which the four vector for current density might be used to introduce an electric current term into the Coulomb force such as to convert it into the Biot-Savart law.[4]
When an electric charge is moving from the perspective of an observer, the electric field of this charge due to space contraction is no longer seen by the observer as spherically symmetric due to non-radial time dilation, and it must be computed using the Lorentz transformations. One of the products of these transformations is the part of the electric field which only acts on moving charges — and we call it the "magnetic field". It is a relativistic manifestation of the more fundamental electric field.
The quantum-mechanical motion of electrons in atoms produces the magnetic fields of permanent ferromagnets. Spinning charged particles also have magnetic moment. Some electrically neutral particles (like the neutron) with non-zero spin also have magnetic moment due to the charge distribution in their inner structure. Particles with zero spin never have magnetic moment which is the consequence that a magnetic field is the result of motion of electric field.
A magnetic field is a vector field: it associates with every point in space a (pseudo) vector that may vary through time. The direction of the field is the equilibrium direction of a magnetic dipole (like a compass needle) placed in the field.
The Lorentz transformation of a spherically-symmetric proper electric field E of a moving electric charge (for example, the electric field of an electron moving in a conducting wire) from the charge's reference frame to the reference frame of a non-moving observer results in the following term which we can define or label as "magnetic field".
Maxwell did much to unify static electricity and magnetism, producing a set of four equations relating the two fields. However, under Maxwell's formulation, there were still two distinct fields describing different phenomena. It was Albert Einstein who showed, using special relativity, that electric and magnetic fields are two aspects of the same thing (a rank-2 tensor), and that one stationary observer may perceive a magnetic force where a moving observer perceives only an electric field. Thus, using special relativity, magnetic forces are a manifestation of electric fields of charges in motion and may be predicted from knowledge of the electric fields and the velocity of movement (relative to some observer) of the charges.
A thought experiment one can do to show this is with two identical infinite and parallel lines of charge having no motion relative to each other but moving together relative to an observer. Another observer is moving alongside the two lines of charge (at the same velocity) and observes only electrostatic repulsive force and acceleration. The first or "stationary" observer seeing the two lines (and second observer) moving past with some known velocity also observes that the "moving" observer's clock is ticking more slowly (due to time dilation) and thus observes the repulsive acceleration of the lines of charge more slowly than that which the "moving" observer sees. The reduction of repulsive acceleration can be thought of as an added attractive force, in a classical electrodynamics context, that reduces the electrostatic repulsive force and also increases in magnitude with increasing velocity. This pseudo-force is precisely the same as the electromagnetic force in a classical context.
A changing magnetic field is mathematically the same as a moving magnetic field (see relativity of motion). Thus, according to Einstein's field transformation equations (that is, the Lorentz transformation of the field from a proper reference frame to a non-moving reference frame), part of it is manifested as an electric field component. This is known as Faraday's law of induction and is the principle behind electric generators and electric motors.
[edit] Magnetic field shapes descriptions
- An azimuthal magnetic field is one that runs east-west.
- A meridional magnetic field is one that runs north-south. In the solar dynamo model of the Sun, differential rotation of the solar plasma causes the meridional magnetic field to stretch into an azimuthal magnetic field, a process called the omega-effect. The reverse process is called the alpha-effect.[5]
- A radial magnetic field is one seen around a straight wire carrying a current. The magnetic field strength decreases with the square of the radial distance from the wire.
- A dipole magnetic field is one seen around a charged particle, or around a bar magnetic.
- A quadruple magnetic field is one seen between two sets (ie four) bar magnets poles. The quadrupole magnet field strength grows linearly with the radial distance from its longitudinal axis.
- A solenoidal magnetic field is similar to a dipole magnetic field, except that a solid bar magnetic is replaces by a hollow electromagnetic coil magnet.
- A toroidal magnetic field occurs in a doughnut-shaped coil, the electric current spiraling around the tube-like surface, and is found, for example, in a tokamak.
- A poloidal magnetic field is generated by a current flowing in a ring, and is found, for example, in a tokamak.