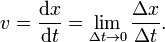Velocity

From Wikipedia, the free encyclopedia

Jump to: navigation, search
This article is about velocity in physics. For other uses, see Velocity (disambiguation).

In physics, velocity is defined as the rate of change of position. It is a vector physical quantity, both speed and direction are required to define it. In the SI (metric) system, it is measured in meters per second (m/s). The scalar absolute value (magnitude) of velocity is speed. For example, "5 metres per second" is a speed and not a vector, whereas "5 metres per second east" is a vector. The average velocity (v) of an object moving through a displacement (Δx) in a straight line during a time interval (Δt) is described by the formula:

v = \frac{\Delta x}{\Delta t}.

Simply put, velocity is displacement per unit of time.

Contents

  • 1 Equations of motion
  • 2 Polar coordinates
  • 3 See also
  • 4 References
  • 5 External links

[edit] Equations of motion

Main article: Equations of motion

The instantaneous velocity vector (v) of an object that has position x(t), at time t, can be computed as the derivative:

v={\mathrm{d}x \over \mathrm{d}t} = \lim_{\Delta t \to 0}{\Delta x \over \Delta t}.

The equation for an object's velocity can be obtained mathematically by taking the integral of the equation for its acceleration beginning from some initial period time t0 to some point in time later tn.

The final velocity v of an object which starts with velocity u and then accelerates at constant acceleration a for a period of time (Δt) is:

v = u + a \Delta t\!

The average velocity of an object undergoing constant acceleration is \begin{matrix} \frac {(u + v)}{2} \; \end{matrix}, where u is the initial velocity and V is the final velocity. To find the displacement, s, of such an accelerating object during a time interval, Δt, then:

\Delta x = \frac {( u + v )}{2}\Delta t.

When only the object's initial velocity is known, the expression,

\Delta x = u \Delta t + \frac{1}{2}a \Delta t^2,

can be used.

This can be expanded to give the position at any time t in the following way:

x(t) = x(0) + \Delta x = x(0) + u \Delta t + \frac{1}{2}a \Delta t^2,

These basic equations for final velocity and displacement can be combined to form an equation that is independent of time, also known as Torricelli's equation:

v^2 = u^2 + 2a\Delta x.\,

The above equations are invalid for both classical mechanics and special relativity. Where classical mechanics and special relativity differ is in how different observers would describe the same situation. In particularly not, in classical mechanics, all observers disagree on the value of m and for position create a situation in which all non-accelerating observers would describe the acceleration of an object with the same values. Neither is true for special relativity. In other words only relative velocity can be calculated.

The kinetic energy (energy of motion), EK, of a moving object is linear with both its mass and the square of its velocity:

E_{K} = \begin{matrix} \frac{1}{2} \end{matrix} mv^2.

The kinetic energy is a scalar quantity.

[edit] Polar coordinates

In polar coordinates, a two-dimensional velocity can be decomposed into a radial velocity, defined as the component of velocity away from or toward the origin (also known as velocity made good), and transverse velocity, the component of velocity along a circle centered at the origin, and equal to the distance to the origin times the angular velocity.

Angular momentum in scalar form is the distance to the origin times the transverse speed, or equivalently, the distance squared times the angular speed, with positive quantities representing counter-clockwise direction and negative quantities representing clockwise direction (in a right-handed coordinate system).

velocity = displacement (divided by) time

If forces are in the radial direction only with an inverse square dependence, as in the case of a gravitational orbit, angular momentum is constant, and transverse speed is inversely proportional to the distance, angular speed is inversely proportional to the distance squared, and the rate at which area is swept out is constant. These relations are known as Kepler's laws of planetary motion