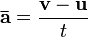Acceleration

From Wikipedia, the free encyclopedia

Jump to: navigation, search
Acceleration is the time rate of change of velocity and/or direction, and at any point on a velocity-time graph, it is given by the slope of the tangent to the curve at that point.

In physics, acceleration is defined as the rate of change of velocity, or, equivalently, as the second derivative of position. It is thus a vector quantity with dimension length/time². In SI units, acceleration is measured in metres/second² (m·s-²). The term "acceleration" generally refers to the change in instantaneous velocity.

Contents

  • 1 Simple Mathematical Explanation
  • 2 Complex Explanation
  • 3 Relation to relativity
  • 4 See also
  • 5 References
  • 6 External links

[edit] Simple Mathematical Explanation

v = {d \over t}

where v is velocity, d is displacement and t is time.

a = {v \over t}

where a is acceleration, v is velocity and t is time.

[edit] Complex Explanation

To accelerate an object is to change its velocity, which is accomplished by altering either its speed or direction (as in the case of uniform circular motion) in relation to time. In this strict mathematical sense, acceleration can have positive and negative values (deceleration). Any time that the sign (+ or -) of the acceleration is the same as the sign of the velocity, the object will speed up. If the signs are opposite, the object will slow down. Acceleration is a vector defined by properties of magnitude (size or measurability) and direction. When either velocity or direction are changed, there is acceleration (or deceleration)


Since the formula for instantaneous velocity is

\vec{v} = {\mathrm{d}\vec{x} \over \mathrm{d}t}.

Then, from the definition of acceleration A = \frac{\Delta v}{\Delta t}, we can ascertain the instantaneous acceleration by use of a limit

A = \lim_{\Delta t\rightarrow 0} \frac{\Delta v}{\Delta t}

by the definition of derivative we have

\lim_{\Delta t\rightarrow 0} \frac{\Delta v}{\Delta t} = \frac{dv}{dt} = \frac{d}{dt}(\frac{dx}{dt}) = \frac{d^2x}{dt^2}

also \mathbf{v}=\int_0^n ({\mathrm{d}\mathbf{v} \over \mathrm{d}t})\,dt OR \mathbf{x}=\int_0^t \mathbf{v}\,dt, i.e. Velocity can be thought of as the integral of acceleration with respect to the time. (Note, this can be a definite or indefinite integration).

\mathbf{a} is the acceleration vector (as acceleration is a vector, it must be described both as a direction and as a magnitude).
v is the velocity function
x is the position function (often confused with displacement (s) which is the change in position )
t is time
d is Leibniz's notation for differentiation
Δ is a symbol that, in this context, means "change in"

When velocity is plotted against time on a velocity vs. time graph, the acceleration is given by the slope, or the derivative of the graph.

If used with SI standard units (metres per second for velocity; seconds for time) this equation gives a the units of m/(s·s), or m/s² (read as "metres per second per second", or "metres per second squared").

An average acceleration, or acceleration over time, ā can be defined as:

\mathbf{\bar{a}} = {\mathbf{v} - \mathbf{u} \over t}

where

u is the initial velocity (m/s)
v is the final velocity (m/s)
t is the time interval (s) elapsed between the two velocity measurements (also written as "Δt")

Transverse acceleration (perpendicular to velocity), as with any acceleration which is not parallel to the direction of motion, causes change in direction. If it is constant in magnitude and changing in direction with the velocity, we get a circular motion. For this centripetal acceleration we have

\mathbf{a} = - \frac{v^2}{r} \frac{\mathbf{r}}{r} = - \omega^2 \mathbf{r}

One common unit of acceleration is g, one g (more specifically, gn or g 0) being the standard uniform acceleration of free fall or 9.80665 m/s², caused by the gravitational field of Earth at sea level at about 45.5° latitude.

Jerk is the rate of change of an object's acceleration over time.

In classical mechanics, acceleration a \ is related to force F \ and mass m \ (assumed to be constant) by way of Newton's second law:

\mathbf{F} = m \cdot \mathbf{a}.

As a result of its invariance under the Galilean transformations, acceleration is an absolute quantity in classical mechanics.

[edit] Relation to relativity

After completing his theory of special relativity, Albert Einstein realized that forces felt by objects undergoing constant proper acceleration are indistinguishable from those in a gravitational field. This was the basis for his development of general relativity, a relativistic theory of gravity.

If you accelerate away from your friend, you could say (given your frame of reference) that it is your friend who is accelerating away from you, although only you feel any force. This is also the basis for the popular Twin paradox, which asks why only one twin ages when moving away from his sibling at near light-speed and then returning, since the aging twin can say that it is the other twin that was moving. General relativity solved the "why does only one object feel accelerated?" problem which had plagued philosophers and scientists since Newton's time (and caused Newton to endorse absolute space). In special relativity, only inertial frames of reference (non-accelerated frames) can be used and are equivalent; general relativity considers all frames, even accelerated ones, to be equivalent. (The path from these considerations to the full theory of general relativity is traced in the Introduction to general relativity.)