Magnetic flux

From Wikipedia, the free encyclopedia

Jump to: navigation, search

Electrostatics

Electromagnetism
Electricity · Magnetism
Electric charge
Coulomb's law
Electric field
Gauss's law
Electric potential
Electric dipole moment
Magnetostatics
Ampère's circuital law
Magnetic field
Magnetic flux
Biot-Savart law
Magnetic dipole moment
Electrodynamics
Electrical current
Lorentz force law
Electromotive force
(EM) Electromagnetic induction
Faraday-Lenz law
Displacement current
Maxwell's equations
(EMF) Electromagnetic field
(EM) Electromagnetic radiation
Electrical Network
Electrical conduction
Electrical resistance
Capacitance
Inductance
Impedance
Resonant cavities
Waveguides
Tensors in Relativity
Electromagnetic tensor
Electromagnetic stress-energy tensor
This box: view • talk • edit

Magnetic flux, represented by the Greek letter Φ (phi), is a measure of quantity of magnetism, taking account of the strength and the extent of a magnetic field. The SI unit of magnetic flux is the weber (in derived units: volt-seconds), and the unit of magnetic flux density is the weber per square meter, or tesla.

[edit] Description

The flux through an element of area perpendicular to the direction of magnetic field is given by the product of the magnetic field and the area element. More generally, magnetic flux is defined by a scalar product of the magnetic field and the area element vector. Gauss's law for magnetism, which is one of the four Maxwell's equations, states that the total magnetic flux through a closed surface is zero. This law is a consequence of the empirical observation that magnetic monopoles do not exist or are not measurable.

The magnetic flux is defined as the integral of the magnetic flux density over an area:

$\Phi_m = \int \!\!\! \int \mathbf{B} \cdot d\mathbf S\,$

where

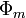$\Phi_m \$ is the magnetic flux

B is the magnetic flux density

S is the area.

We know from Gauss's law for magnetism that

$\nabla \cdot \mathbf{B}=0.\,$

The volume integral of this equation, in combination with the divergence theorem, provides the following result:

$\int \!\!\! \int \!\!\! \int_V \nabla \cdot \mathbf{B} \, d\tau = \oint \!\!\! \oint_{\partial V} \mathbf{B} \cdot d\mathbf{S}=0.$

In other words, the magnetic flux through any closed surface must be zero; there are no "magnetic charges".

By way of contrast, Gauss's law for electric fields, another of Maxwell's equations, is

$\nabla \cdot \mathbf{E} = {\rho \over \epsilon_0},$

where

E is the electric field,

ρ

is the free electric charge density, (not including dipole charges bound in a material),

ε 0

is the permittivity of free space.

Note that this indicates the presence of electric monopoles, that is, free positive or negative charges.

The direction of the magnetic field vector $\mathbf{B}$ is by definition from the south to the north pole of a magnet (within the magnet). Outside of the magnet, the field lines will go from north to south.

A change of magnetic flux through a loop of conductive wire will cause an emf, and therefore an electric current, in the loop. The relationship is given by Faraday's law:

$\mathcal{E} = \oint \mathbf{E} \cdot d\mathbf{s} = -{d\Phi_m \over dt}.$

This is the principle behind an electrical generator.