Rigid body
From Wikipedia, the free encyclopedia
In physics, a rigid body is an idealization of a solid body of finite size in which deformation is neglected. In other words, the distance between any two given points of a rigid body remains constant in time regardless of external forces exerted on it. In classical mechanics a rigid body is usually considered as a continuous mass distribution, while in quantum mechanics a rigid body is usually thought of as a collection of point masses. For instance, in quantum mechanics molecules (consisting of the point masses: electrons and nuclei) are often seen as rigid bodies (see classification of molecules as rigid rotors).
Contents
|
[edit] Kinematics
[edit] Position
The position of a rigid body can be described by a combination of a translation and a rotation from a given reference position. For this purpose a reference frame is chosen that is rigidly connected to the body (see also below). This is typically referred to as a "local" reference frame (L). The position of its origin and the orientation of its axes with respect to a given "global" or "world" reference frame (G) represent the position of the body. The position of G not necessarily coincides with the initial position of L.
Thus, the position of a rigid body has two components: linear and angular, respectively. Each can be represented by a vector. The angular position is also called orientation. There are several methods to describe numerically the orientation of a rigid body (see orientation). In general, if the rigid body moves, both its linear and angular position vary with time. In the kinematic sense, these changes are referred to as translation and rotation, respectively.
All the points of the body change their position during a rotation about a fixed axis, except for those lying on the rotation axis. If the rigid body has any rotational symmetry, not all orientations are distinguishable, except by observing how the orientation evolves in time from a known starting orientation.
In two dimensions the situation is similar. In one dimension a "rigid body" can not move (continuously change) from one orientation to the other.
[edit] Other quantities
If C is the origin or the local reference frame L,
- the (linear or translational) velocity of a rigid body is defined as the velocity of C;
- the (linear or translational) acceleration of a rigid body is defined as the acceleration of C;
- the angular (or rotational) velocity of a rigid body is defined as the time derivative of its angular position (see angular velocity of a rigid body);
- the angular (or rotational) acceleration of a rigid body is defined as the time derivative of its angular velocity.
For any point/particle of a moving rigid body we have
where
 represents the position of the point/particle with respect to the reference point of the body in terms of the local frame L (the rigidity of the body means that this does not depend on time)
represents the position of the point/particle with respect to the reference point of the body in terms of the local frame L (the rigidity of the body means that this does not depend on time) represents the position of the point/particle at time
represents the position of the point/particle at time 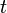
 represents the position of the reference point of the body (the origin of local frame L) at time
represents the position of the reference point of the body (the origin of local frame L) at time 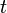
 is the orientation matrix, an orthogonal matrix with determinant 1, representing the orientation (angular position) of the local frame L, with respect to the arbitrary reference orientation of frame G. Think of this matrix as three orthogonal unit vectors, one in each column, which define the orientation of the axes of frame L with respect to G.
is the orientation matrix, an orthogonal matrix with determinant 1, representing the orientation (angular position) of the local frame L, with respect to the arbitrary reference orientation of frame G. Think of this matrix as three orthogonal unit vectors, one in each column, which define the orientation of the axes of frame L with respect to G. represents the angular velocity
represents the angular velocity represents the total velocity of the point/particle
represents the total velocity of the point/particle represents the translational velocity (i.e. the velocity of the origin of frame L)
represents the translational velocity (i.e. the velocity of the origin of frame L)
In 2D the angular velocity is a scalar, and matrix A(t) simply represents a rotation in the xy-plane by an angle which is the integral of the angular velocity over time.
Vehicles, walking people, etc. usually rotate according to changes in the direction of the velocity: they move forward with respect to their own orientation. Then, if the body follows a closed orbit in a plane, the angular velocity integrated over a time interval in which the orbit is completed once, is an integer times 360°. This integer is the winding number with respect to the origin of the velocity. Compare the amount of rotation associated with the vertices of a polygon.
[edit] Dynamics
Any point that is rigidly connected to the body can be used as reference point (origin of frame L) to describe the linear motion of the body (the linear position, velocity and acceleration vectors depend on the choice).
However, depending on the application, a convenient choice may be:
- the center of mass of the whole system;
- a point such that the translational motion is zero or simplified, e.g on an axle or hinge, at the center of a ball-and-socket joint, etc.
When the center of mass is used as reference point:
- The (linear) momentum is independent of the rotational motion. At any time it is equal to the total mass of the rigid body times the translational velocity.
- The angular momentum with respect to the center of mass is the same as without translation: at any time it is equal to the inertia tensor times the angular velocity. When the angular velocity is expressed with respect to the principal axes frame of the body, each component of the angular momentum is a product of a moment of inertia (a principal value of the inertia tensor) times the corresponding component of the angular velocity; the torque is the inertia tensor times the angular acceleration.
- Possible motions in the absence of external forces are translation with constant velocity, steady rotation about a fixed principal axis, and also torque-free precession.
- The net external force on the rigid body is always equal to the total mass times the translational acceleration (i.e., Newton's second law holds for the translational motion, even when the net external torque is nonnull, and/or the body rotates).
- The total kinetic energy is simply the sum of translational and rotational energy.
[edit] Geometry
Two rigid bodies are said to be different (not copies) is that there is no proper rotation from one to the other. A rigid body is called chiral if its mirror image is different in that sense, i.e., if it has either no symmetry or its symmetry group contains only proper rotations. In the opposite case an object is called achiral: the mirror image is a copy, not a different object. Such an object may have a symmetry plane, but not necessarily: there may also be a plane of reflection with respect to which the image of the object is a rotated version. The latter applies for S2n, of which the case n = 1 is inversion symmetry.
For a (rigid) rectangular transparent sheet, inversion symmetry corresponds to having on one side an image without rotational symmetry and on the other side an image such that what shines through is the image at the top side, upside down. We can distinguish two cases:
- the sheet surface with the image is not symmetric - in this case the two sides are different, but the mirror image of the object is the same, after a rotation by 180° about the axis perpendicular to the mirror plane.
- the sheet surface with the image has a symmetry axis - in this case the two sides are the same, and the mirror image of the object is also the same, again after a rotation by 180° about the axis perpendicular to the mirror plane.
A sheet with a through and through image is achiral. We can distinguish again two cases:
- the sheet surface with the image has no symmetry axis - the two sides are different
- the sheet surface with the image has a symmetry axis - the two sides are the same
[edit] Configuration space
The configuration space of a rigid body with one point fixed (i.e., a body with zero translational motion) is given by the underlying manifold of the rotation group SO(3). The configuration space of a nonfixed (with non-zero translational motion) rigid body is E+(3), the subgroup of direct isometries of the Euclidean group in three dimensions (combinations of translations and rotations).


