Kinematics

From Wikipedia, the free encyclopedia

Jump to: navigation, search

Kinematics (Greek κινειν,kiein, to move) is a branch of mechanics which describes the motion of objects without the consideration of the masses or forces that bring about the motion. In contrast, dynamics is concerned with the forces and interactions that produce or affect the motion.

Kinematics studies how the position of an object changes with time. Position is measured with respect to a set of coordinates. Velocity is the rate of change of position. Acceleration is the rate of change of velocity. Velocity and Acceleration are the two principal quantities which describe how position changes.

The simplest application of kinematics is to point particle motion (translational kinematics or linear kinematics). The description of rotation (rotational kinematics or angular kinematics) is more complicated. The state of a generic rigid body may be described by combining both translational and rotational kinematics (rigid-body kinematics). A more complicated case is the kinematics of a system of rigid bodies, possibly linked together by mechanical joints. The kinematic description of fluid flow is even more complicated, and not generally thought of in the context of kinematics.


Contents

  • 1 Translational motion
    • 1.1 Relative velocity
    • 1.2 Equations of uniformly accelerated motion
    • 1.3 Example: Rectilinear (1D) motion
      • 1.3.1 How long will it be airborne?
      • 1.3.2 What altitude will it reach before it begins to fall?
      • 1.3.3 What will its final velocity be when it reaches the ground?
    • 1.4 Example: Projectile (2D) motion
      • 1.4.1 How far will it travel before hitting the ground?
  • 2 Rotational motion
  • 3 Coordinate systems
    • 3.1 Fixed rectangular coordinates
    • 3.2 Two dimensional rotating reference frame
      • 3.2.1 Derivatives of unit vectors
      • 3.2.2 Position, velocity, and acceleration
        • 3.2.2.1 Position
        • 3.2.2.2 Velocity
        • 3.2.2.3 Acceleration
    • 3.3 Three dimensional rotating coordinate frame
  • 4 Kinematic constraints
    • 4.1 Rolling without slipping
    • 4.2 Inextensible cord
  • 5 See also
  • 6 External links

[edit] Translational motion

Translational (or linear) kinematics is the description of the motion in space of a point along a trajectory (which can be rectilinear or curved) and involves the definition and use of the following three quantities:

(Linear) Position: (Linear) Velocity: (Linear) Acceleration: (to be written)

[edit] Relative velocity

Main article: Relative velocity

To describe the motion of object A with respect to object O, when we know how each is moving with respect to object B, we use the following equation involving vectors and vector addition:

r_{A/O} = r_{B/O} + r_{A/B} \,\!

The above relative motion equation states that the motion of A relative to O is equal to the motion of B relative to O plus the motion of A relative to B.

For example, let Ann move with velocity VA and let Bob move with velocity VB, each velocity given with respect to the ground. To find how fast Ann is moving relative to Bob (we call this velocity VA / B), the equation above gives:

V_{A} = V_{B} + V_{A/B} \,\! .

To find VA / B we simply rearrange this equation to obtain:

V_{A/B} = V_{A} -V_{B} \,\! .

At velocities comparable to the speed of light, these equations of relative motions are found through Einstein's theory of special relativity rather than the above equation of relative motion.

[edit] Equations of uniformly accelerated motion

An object moving with constant acceleration is said to be undergoing uniformly accelerated motion (UAM). Its motion can be described with four simple algebraic equations:

\,x_f - x_i = v_i t + \frac{1}{2} at^2 \qquad x_f - x_i = \frac{1}{2} (v_f + v_i)t
\,v_f = v_i + a t \qquad v_f^2 = v_i^2 + 2 a (x_f - x_i)

where vi and vf are the initial and final velocities, xi and xf are the initial and final positions on a reference axis, a is the constant acceleration, and t is the timespan between the initial and final positions.

[edit] Example: Rectilinear (1D) motion

An object is fired upwards, reaches its apex, and then begins its descent under a constant acceleration of -9.81 m/s2.

Consider an object which is fired directly upwards and falls back to the ground so that its trajectory is contained in a straight line. If we adopt the convention that the upward direction is the positive direction, the object experiences a constant acceleration of approximately -9.81 m/s2. Therefore, its motion can be modeled with the equations governing uniformly accelerated motion.

There are several interesting kinematic questions we can ask about the particles motion: How long will it be airborne? What altitude will it reach before it begins to fall? What will its final velocity be when it reaches the ground? For the sake of example, assume the object has an initial velocity of +50 m/s.

[edit] How long will it be airborne?

To answer this question, we apply the formula

x_f - x_i = v_i t + \frac{1}{2} at^2.

Since the question asks for the length of time between the object leaving the ground and hitting the ground on its fall, the displacement is zero.

0 = v_i t + \frac{1}{2} at^2 = t(v_i + \frac{1}{2} at)

We find two solutions for it. The trivial solution says the time is zero; this is actually also true, it is the first moment the displacement is zero: just when it starts motion. However, the solution of interest is

t = -\frac{2v_i}{a} = -\frac{2*50}{-9.81} = 10.2 \ s

[edit] What altitude will it reach before it begins to fall?

In this case, we use the fact that the object has a velocity of zero at the apex of its trajectory. Therefore, the applicable equation is:

v_f^2 = v_i^2 + 2 a (x_f - x_i)

If the origin of our coordinate system is at the ground, then xi is zero. Then we solve for xf and substitute known values:

x_f = \frac{v_f^2 - v_i^2}{2 a} + x_i = \frac{0-50^2}{2*-9.81}+0 = 127.55 \ m

[edit] What will its final velocity be when it reaches the ground?

To answer this question, we use the fact that the object has an initial velocity of zero at the apex before it begins its descent. We can use the same equation we used for the last question, using the value of 127.55 m for xi.

v_f = \sqrt{v_i^2 + 2 a (x_f - x_i)} = \sqrt{0^2 + 2 (-9.81) (0 - 127.55)} = 50\ m/s

We find that the final and initial speeds are equal, a result which agrees with conservation of energy.

[edit] Example: Projectile (2D) motion

An object fired at an angle θ from the ground follows a parabolic trajectory.

Suppose that an object is not fired vertically but is fired at an angle θ from the ground. The object will then follow a parabolic trajectory, and its horizontal motion can be modeled independently of its vertical motion. Assume that the object is fired at an initial velocity of 50 m/s and 30 degrees from the horizontal.

[edit] How far will it travel before hitting the ground?

The object experiences an acceleration of -9.81 m/s2 in the vertical direction and no acceleration in the horizontal direction. Therefore, the horizontal displacement is

\Delta x = x_f - x_i = v_i \cos \theta \ t + \frac{1}{2} at^2 = v_i \cos \theta \ t

In order to solve this equation, we must find t. This can be done by analyzing the motion in the vertical direction. If we impose that the vertical displacement is zero, we can use the same procedure we did for rectilinear motion to find t.

0 = v_i \sin \theta \ t + \frac{1}{2} at^2 = t(v_i \sin \theta + \frac{1}{2} at)

We now solve for t and substitute this expression into the original expression for horizontal displacement. (Note the use of the trigonometric identity 2sinθcosθ = sin2θ)

\Delta x = v_i \cos \theta \left(\frac{-2 v_i \sin \theta}{a}\right) = -\frac{v_i^2 \sin 2\theta}{a} = 220.70 \ m

[edit] Rotational motion

The angular velocity vector points up for counterclockwise rotation and down for clockwise rotation, as specified by the right-hand rule.

Rotational kinematics is the description of the rotation of an object and involves the definition and use of the following three quantities:

Angular position: If a vector is defined as the oriented distance from the axis of rotation to a point on an object, the angular position of that point is the oriented angle &theta from a reference axis (e.g. the positive x-semiaxis) to that vector. An oriented angle is an angle swept about a known rotation axis and in a known rotation sense. In two-dimensional kinematics (the description of planar motion), the rotation axis is normal to the reference frame and can be represented by a rotation point (or center), and the rotation sense is represented by the sign of the angle (typically, a positive sign means counterclockwise sense). Angular displacement can be regarded as a relative position. It is represented by the oriented angle swept by the above mentioned point (or vector), from an angular position to another.

Angular velocity: The magnitude of the angular velocity ω is the rate at which the angular position θ changes with respect to time t:

\mathbf{\omega} = \frac {\mathrm{d}\theta}{\mathrm{d}t}

Angular acceleration: The magnitude of the angular acceleration α is the rate at which the angular velocity ω changes with respect to time t:

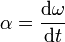
\mathbf{\alpha} = \frac {\mathrm{d}\mathbf{\omega}}{\mathrm{d}t}

The equations of translational kinematics can easily be extended to planar rotational kinematics with simple variable exchanges:

\,\!\theta_f - \theta_i = \omega_i t + \frac{1}{2} \alpha t^2 \qquad \theta_f - \theta_i = \frac{1}{2} (\omega_f + \omega_i)t
\,\!\omega_f = \omega_i + \alpha t \qquad \alpha = \frac{\omega_f - \omega_i}{t} \qquad \omega_f^2 = \omega_i^2 + 2 \alpha (\theta_f - \theta_i)

.

Here \,\!\theta_i and \,\!\theta_f are, respectively, the initial and final angular positions, \,\!\omega_i and \,\!\omega_f are, respectively, the initial and final angular velocities, and \,\!\alpha is the constant angular acceleration. Although position in space and velocity in space are both true vectors (in terms of their properties under rotation), as is angular velocity, angle itself is not a true vector.

[edit] Coordinate systems

In any given situation, the most useful coordinates may be determined by constraints on the motion, or by the geometrical nature of the force causing or affecting the motion. Thus, to describe the motion of a bead constrained to move along a circular hoop, the most useful coordinate may be its angle on the hoop. Similarly, to describe the motion of a particle acted upon by a central force, the most useful coordinates may be polar coordinates.

[edit] Fixed rectangular coordinates

In this coordinate system, vectors are expressed as an addition of vectors in the x, y, and z direction from a non-rotating origin. Usually i is a unit vector in the x direction, j is a unit vector in the y direction, and k is a unit vector in the z direction.

The position vector, s (or r), the velocity vector, v, and the acceleration vector, a are expressed using rectangular coordinates in the following way:

\vec s = x \vec i + y \vec j + z \vec k \, \!

\vec v = \dot {s} = \dot {x} \vec {i} + \dot {y} \vec {j} + \dot {z} \vec {k} \, \!

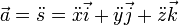
\vec a = \ddot {s} = \ddot {x} \vec {i} + \ddot {y} \vec {j} + \ddot {z} \vec {k} \, \!

Note: \dot {x} = \frac{\mathrm{d}x}{\mathrm{d}t} , \ddot {x} = \frac{\mathrm{d}^2x}{\mathrm{d}t^2}

[edit] Two dimensional rotating reference frame

This coordinate system only expresses planar motion.

This system of coordinates is based on three orthogonal unit vectors: the vector i, and the vector j which form a basis for the plane in which the objects we are considering reside, and k about which rotation occurs. Unlike rectangular coordinates, which are measured relative to an origin that is fixed and non rotating, the origin of these coordinates can rotate and translate - often following a particle on a body that is being studied.

[edit] Derivatives of unit vectors

The position, velocity, and acceleration vectors of a given point can be expressed using these coordinate systems, but we have to be a bit more careful than we do with fixed frames of reference. Since the frame of reference is rotating, we must take the derivatives of the unit vectors into account when taking the derivative of any of these vectors. If the coordinate frame is rotating at a rate of ω in the counterclockwise direction (that's ωk using the right hand rule) then the derivatives of the unit vectors are as follows:

\dot{\vec i} = \omega \vec k \times \vec i = \omega \vec j

\dot{\vec j} = \omega \vec k \times \vec j = - \omega \vec i

[edit] Position, velocity, and acceleration

Given these identities, we can now figure out how to represent the position, velocity, and acceleration vectors of a particle using this reference frame.

[edit] Position

Position is straightforward:

\vec s = x \vec j

It is just the distance from the origin in the direction of each of the unit vectors.

[edit] Velocity

Velocity is the time derivative of position:

\vec v = \frac{\mathrm{d}\vec s}{\mathrm{d}t} = \frac{\mathrm{d} (x \vec i)}{\mathrm{d}t} + \frac{\mathrm{d} (y \vec j)}{\mathrm{d}t}

By the product rule, this is:

\vec v = \dot x \vec i + x \dot{\vec i} + \dot y \vec j + y \dot{\vec j}

Which from the identities above we know to be:

\vec v = \dot x \vec i + x \omega \vec j + \dot y \vec j - y \omega \vec i = (\dot x - y \omega) \vec i + (\dot y + x \omega) \vec j

or equivalently

\vec v = (\dot x \vec i + \dot y \vec j) + (y \dot{\vec j} + x \dot{\vec i}) = \vec v_{rel} + \vec \omega \times \vec r

where \vec v_{rel} is the velocity of the particle relative to the coordinate system.

[edit] Acceleration

Acceleration is the time derivative of velocity.

We know that:

\vec a = \frac{\mathrm{d} \vec v}{\mathrm{d}t} = \frac{\mathrm{d} \vec v_{rel}}{\mathrm{d}t} + \frac{\mathrm{d} (\vec \omega \times \vec r)}{\mathrm{d}t}

Consider the \frac{\mathrm{d} \vec v_{rel}}{\mathrm{d}t} part. \vec v_{rel} has two parts we want to find the derivative of: the relative change in velocity (\vec a_{rel}), and the change in the coordinate frame (\omega \times \vec v_{rel}).

\frac{\mathrm{d} \vec v_{rel}}{\mathrm{d}t} = \vec a_{rel} + \omega \times \vec v_{rel}

Next, consider \frac{\mathrm{d} (\vec \omega \times \vec r)}{\mathrm{d}t}. Using the chain rule:

\frac{\mathrm{d} (\vec \omega \times \vec r)}{\mathrm{d}t} = \dot{\vec \omega} \times \vec r + \vec \omega \times \dot{\vec r}

\dot{\vec r} we know from above:

\frac{\mathrm{d} (\vec \omega \times \vec r)}{\mathrm{d}t} = \dot{\vec \omega} \times \vec r + \vec \omega \times (\vec \omega \times \vec r) + \vec \omega \times \vec v_{rel}

So all together:

\vec a = \vec a_{rel} + \omega \times \vec v_{rel} + \dot{\vec \omega} \times \vec r + \vec \omega \times (\vec \omega \times \vec r) + \vec \omega \times \vec v_{rel}

And collecting terms:

\vec a = \vec a_{rel} + 2(\omega \times \vec v_{rel}) + \dot{\vec \omega} \times \vec r + \vec \omega \times (\vec \omega \times \vec r)

[edit] Three dimensional rotating coordinate frame

(to be written)

[edit] Kinematic constraints

A kinematic constraint is any condition relating properties of a dynamic system that must hold true at all times. Below are some common examples:

[edit] Rolling without slipping

An object that rolls against a surface without slipping obeys the condition that the velocity of its center of mass is equal to the cross product of its angular velocity with a vector from the point of contact to the center of mass, :

v_G(t) = \omega \times r_{G/O} \,\!

For the case of an object that does not tip or turn, this reduces to v = R ω .

[edit] Inextensible cord

This is the case where bodies are connected by some cord that remains in tension and cannot change length. The constraint is that the sum of all components of the cord, however they are defined, is the total length, and the time derivative of this sum is zero.