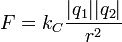Coulomb's law
From Wikipedia, the free encyclopedia
| Electromagnetism | |
| Electricity · Magnetism | |
| Electrostatics | |
|---|---|
| Electric charge | |
| Coulomb's law | |
| Electric field | |
| Gauss's law | |
| Electric potential | |
| Electric dipole moment | |
| Magnetostatics | |
| Ampère's circuital law | |
| Magnetic field | |
| Magnetic flux | |
| Biot-Savart law | |
| Magnetic dipole moment | |
| Electrodynamics | |
| Electrical current | |
| Lorentz force law | |
| Electromotive force | |
| (EM) Electromagnetic induction | |
| Faraday-Lenz law | |
| Displacement current | |
| Maxwell's equations | |
| (EMF) Electromagnetic field | |
| (EM) Electromagnetic radiation | |
| Electrical Network | |
| Electrical conduction | |
| Electrical resistance | |
| Capacitance | |
| Inductance | |
| Impedance | |
| Resonant cavities | |
| Waveguides | |
| Tensors in Relativity | |
| Electromagnetic tensor | |
| Electromagnetic stress-energy tensor | |
Coulomb's law, developed in the 1780s by French physicist Charles Augustin de Coulomb, may be stated as follows:
The magnitude of the electrostatic force between two point electric charges is directly proportional to the product of the magnitudes of each charge and inversely proportional to the square of the distance between the charges.
Contents
|
[edit] Scalar form
If one is interested only in the magnitude of the force, and not in its direction, it may be easiest to consider a simplified, scalar version of the law:
where:
 is the magnitude of the force exerted,
is the magnitude of the force exerted, is the charge on one body,
is the charge on one body,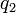 is the charge on the other body,
is the charge on the other body, is the distance between them,
is the distance between them, 8.988×109 N m2 C−2 (also m F−1) is the electrostatic constant or Coulomb force constant (the number is the square of the speed of light in km/s, divided by 10), and
8.988×109 N m2 C−2 (also m F−1) is the electrostatic constant or Coulomb force constant (the number is the square of the speed of light in km/s, divided by 10), and 8.854×10−12 C2 N−1 m−2 (also F m−1) is the permittivity of free space, also called electric constant, an important physical constant.
8.854×10−12 C2 N−1 m−2 (also F m−1) is the permittivity of free space, also called electric constant, an important physical constant.
In cgs units, the unit charge, esu of charge or statCoulomb, is defined so that this Coulomb force constant is 1.
This formula says that the magnitude of the force is directly proportional to the magnitude of the charges of each object and inversely proportional to the square;of the distance between them. When measured in units that people commonly use (such as MKS - see International System of Units), the Coulomb force constant, k, is numerically much much larger than the universal gravitational constant G. This means that for objects with charge that is of the order of a unit charge (C) and mass of the order of a unit mass (kg), the electrostatic forces will be so much larger than the gravitational forces that the latter force can be ignored. This is not the case when Planck units are used and both charge and mass are of the order of the unit charge and unit mass. However, charged elementary particles have mass that is far less than the Planck mass while their charge is about the Planck charge so that, again, gravitational forces can be ignored. For example, the electrostatic force between an electron and a proton, which constitute a hydrogen atom, is about 40 orders of magnitude greater compared to the gravitational force between them.
The force F acts on the line connecting the two charged objects. Charged objects of the same polarity repel each other along this line and charged objects of opposite polarity attract each other along this line connecting them.
Coulomb's law can also be interpreted in terms of atomic units with the force expressed in Hartrees per Bohr radius, the charge in terms of the elementary charge, and the distances in terms of the Bohr radius.
[edit] Electric field
It follows from the Lorentz Force Law that the magnitude of the electric field E created by a single point charge q is
For a positive charge q, the direction of E points along lines directed radially away from the location of the point charge, while the direction is the opposite for a negative charge. Units: volts per meter or newtons per coulomb.
[edit] Vector form
For the direction and magnitude of the force simultaneously, one will wish to consult the full vector;version of Coulomb's Law:
where
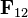 is the electrostatic force vector, for the force experienced by charge 1 from the action of charge 2.
is the electrostatic force vector, for the force experienced by charge 1 from the action of charge 2. is the charge on which the force acts,
is the charge on which the force acts,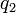 is the acting charge,
is the acting charge, is the vector pointing from charge 2 to charge 1,
is the vector pointing from charge 2 to charge 1, is position vector of
is position vector of  ,
, is position vector of
is position vector of 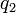 ,
, is the the magnitude of
is the the magnitude of 
 is a unit vector pointing in the direction of
is a unit vector pointing in the direction of  , and
, and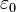 is a constant called the permittivity of free space.
is a constant called the permittivity of free space.
This vector equation indicates that opposite charges attract, and like charges repel. When  is negative, the force is attractive. When positive, the force is repulsive.
is negative, the force is attractive. When positive, the force is repulsive.
[edit] Graphical representation
Below is a graphical representation of Coulomb's law, when  . The vector
. The vector  is the force experienced by
is the force experienced by  . The vector
. The vector  is the force experienced by
is the force experienced by 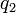 . Their magnitudes will always be equal. The vector
. Their magnitudes will always be equal. The vector  is the displacement vector between two charges (
is the displacement vector between two charges ( and
and 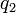 ).
).
[edit] Electrostatic approximation
In either formulation, Coulomb's law is fully accurate only when the objects are stationary, and remains approximately correct only for slow movement. These conditions are collectively known as the electrostatic approximation. When movement takes place, magnetic fields are produced which alter the force on the two objects. The magnetic interaction between moving charges may be thought of as a manifestation of the force from the electrostatic field but with Einstein's theory of relativity taken into consideration.
The accuracy of the exponent in Coulomb's Law has been found to differ from two by less than one in a billion by measuring the electric field inside a charged conducting shell.
[edit] Table of derived quantities
| Particle property | Relationship | Field property | |||||
| Vector quantity |
|  |
| ||||
| Relationship |  |  | |||||
| Scalar quantity |
|  |
|