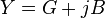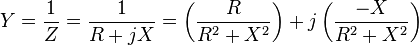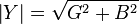Susceptance

From Wikipedia, the free encyclopedia

Jump to: navigation, search

In electrical engineering, the susceptance (B) is the imaginary part of the admittance. In SI units, the susceptance is measured in siemens. Oliver Heaviside first defined this property, which he called permittance, in June 1887.

[edit] Formula

The general equation defining admittance is given by

$Y = G + j B \,$

where

Y is the admittance, measured in siemens,

G is the conductance, measured in siemens,

j is the imaginary unit, and

B is the susceptance, measured in siemens.

Rearranging yields

$B = \frac{Y - G} {j}$ .

But since

$\frac{1}{j} =\frac{j}{j \cdot j} = \frac{j}{-1} = -j$ ,

we obtain

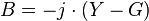$B = -j \cdot (Y -G)$ .

The admittance (Y) is the inverse of the impedance (Z)

$Y = \frac {1} {Z} = \frac {1} {R + j X} = \left( \frac {R} {R^2+X^2} \right) + j \left( \frac{-X} {R^2+X^2} \right) \,$

$B = Im(Y) = \left( \frac{-X} {R^2+X^2} \right)$

where

$Z = R + j X \,$

Z is the impedance, measured in ohms

R is the resistance, measured in ohms

X is the reactance, measured in ohms.

Note: The susceptance is the imaginary part of the admittance.

The magnitude of admittance is given by:

$\left | Y \right | = \sqrt {G^2 + B^2} \,$