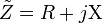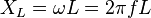Reactance

From Wikipedia, the free encyclopedia

Jump to: navigation, search

This article is about electronics. For a discussion of "reactive" or "reactance" in chemistry, see reactivity.

For a discussion of the psychological concept of reactance, see reactance (psychology).

Reactance is the imaginary part of electrical impedance, a measure of opposition to a sinusoidal alternating current. Reactance arises from the presence of inductance and capacitance within a circuit, and is denoted by the symbol 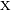$\scriptstyle{\Chi}$ , the SI unit is the ohm.

Both reactance 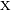$\scriptstyle{\Chi}$ and resistance 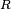$\scriptstyle{R}$ are required to determine the impedance $\scriptstyle{\tilde{Z}}$ ; although in some circumstances the reactance may dominate the impedance, at least an approximate knowledge of the resistance is required to establish this.

$\tilde{Z} = R + j\Chi$

Both the magnitude $\scriptstyle{|\tilde{Z}|}$ and the phase $\scriptstyle{\theta}$ of the impedance depend on both the resistance and the reactance.

$|\tilde{Z}| = \sqrt{ZZ^*} = \sqrt{R^2 + \Chi^2}$

$\theta = \arctan{\left({\Chi \over R}\right)}$

The magnitude is the ratio of the voltage and current amplitudes, while the phase is the voltage–current phase difference.

If $\scriptstyle{\Chi > 0}$ , the reactance is said to be inductive
If $\scriptstyle{\Chi = 0}$ , then the impedance is purely resistive
If $\scriptstyle{\Chi < 0}$ , the reactance is said to be capacitive

1 Physical significance
2 Capacitive reactance
3 Inductive reactance
4 Phase relationship
5 References
6 See also
7 External links

[edit] Physical significance

Determining the voltage-current relationship requires knowledge of both the resistance and the reactance. The reactance on its own gives only limited physical information about an electrical component or network:

The value of the reactance is a lower limit on the magnitude of the impedance
A positive reactance implies that the phase of the voltage leads the phase of the current, while a negative reactance implies that the phase of the voltage lags the phase of the current
A reactance of zero implies the current and voltage are in phase (the only situation in which a specific value for the either the magnitude or phase of the impedance can be determined with knowledge of only the reactance) and conversely if the reactance is non-zero then there is a phase difference between the voltage and current

There are certain specific quantities that depend on the reactance alone, for example; resonance in an RLC circuit occurs when the reactive impedances Z_C and Z_L cancel. This means that the impedance has a phase of zero (a specific example of the third point above).

[edit] Capacitive reactance

Main article: Capacitance

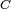Capacitive reactance $\scriptstyle{\Chi_C}$ is inversely proportional to the signal frequency $\scriptstyle{f}$ and the capacitance $\scriptstyle{C}$ .

$\Chi_C = -\frac {1} {\omega C} = -\frac {1} {2\pi f C}\quad$

A capacitor consists of two conductors separated by an insulator, also known as a dielectric.

At low frequencies a capacitor is open circuit, as no current flows in the dielectric. A DC voltage applied across a capacitor causes charge to accumulate on one side, the electric field due to the accumulated charge is the source of the opposition to the flow of current. When the potential associated with the charge exactly balances the applied voltage, the current goes to zero.

Driven by an AC supply a capacitor will only accumulate a limited amount of charge before the potential difference changes sign and the charge dissipates. The higher the frequency, the less charge will accumulate and the smaller the opposition to the flow of current.

[edit] Inductive reactance

Main article: Inductance

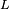Inductive reactance $\scriptstyle{\Chi_L}$ is proportional to the signal frequency $\scriptstyle{f}$ and the inductance $\scriptstyle{L}$ .

$X_L = \omega L = 2\pi f L\quad$

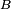An inductor consists of a coiled conductor. Faraday's law of electromagnetic induction gives the back emf $\scriptstyle{\mathcal{E}}$ (voltage opposing current) due to a rate-of-change of magnetic flux density $\scriptstyle{B}$ through a current loop.

$\mathcal{E} = -{{d\Phi_B} \over dt}\quad$

For an inductor consisting of a coil with $N$ loops this gives.

$\mathcal{E} = -N{d\Phi_B \over dt}\quad$

The back-emf is the source of the opposition to current flow. A constant direct current has a zero rate-of-change, and sees an inductor as a short-circuit (it is typically made from a material with a low resistivity). An alternating current has a time-averaged rate-of-change that is proportional to frequency, this causes the increase in inductive reactance with frequency.

[edit] Phase relationship

The phase of the voltage across a purely reactive device (a device with a resistance of zero) lags the current by $\scriptstyle{\pi/2}$ for a capacitive reactance and leads the current by $\scriptstyle{\pi/2}$ for an inductive reactance. Note that without knowledge of both the resistance and reactance we cannot determine the voltage--current relationships.

The origin of the different signs for capacitive and inductive reactance is the phase factor in the impedance.

$\tilde{Z}_C = {1 \over \omega C}e^{j(-{\pi \over 2})} = j\left(-{1 \over \omega C}\right) = j\Chi_C\quad$

$\tilde{Z}_L = \omega Le^{j{\pi \over 2}} = j\omega L = j\Chi_L\quad$