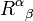Electromagnetic wave equation
From Wikipedia, the free encyclopedia
The electromagnetic wave equation is a second-order partial differential equation that describes the propagation of electromagnetic waves through a medium or in a vacuum. The homogeneous form of the equation, written in terms of either the electric field E or the magnetic field H, takes the form:
where c is the speed of light in the medium. In a vacuum, c = 2.998 x 108 meters per second, which is the speed of light in free space.
The electromagnetic wave equation derives from Maxwell's equations.
In a linear, isotropic, non-dispersive medium, the magnetic flux density B is related to the magnetic field H by
where μ is the magnetic permeability of the medium.
It should also be noted that in most modern literature, B is called the "magnetic field," and H is called either the "auxiliary magnetic field," or "the H vector."
In this article, it is most appropriate to use SI units through the motivation and derivation of the homogeneous wave equation. Once the marriage between electromagnetism and light has been made, and the relationship between the permitivity/permeability and the speed of light has been derived, it is often useful to use other units, such as cgs or Lorentz-Heaviside. At that point, we display results in all three sets of units.
Contents
|
[edit] Speed of propagation
[edit] In vacuum
If the wave propagation is in vacuum, then
 meters per second
meters per second
is the speed of light in vacuum. The vacuum permeability  and the vacuum permittivity
and the vacuum permittivity  are important physical constants that play a key role in electromagnetic theory.
are important physical constants that play a key role in electromagnetic theory.
| Symbol | Name | Numerical Value | SI Unit of Measure | Type |
|---|---|---|---|---|
 | Speed of light in vacuum |  | meters per second | defined |
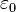 | electric constant |  | farads per meter | derived |
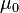 | magnetic constant |  | henries per meter | defined |
[edit] In a material medium
For the purposes of this article, we will assume that all materials are linear, isotropic, and non-dispersive. In that case, the speed of light in a material medium is
where
is the refractive index of the medium,  is the magnetic permeability of the medium, and
is the magnetic permeability of the medium, and  is the electric permittivity of the medium.
is the electric permittivity of the medium.
[edit] The origin of the electromagnetic wave equation
[edit] Conservation of charge
Conservation of charge requires that the time rate of change of the total charge enclosed within a volume V must equal the net current flowing into the surface S enclosing the volume:
where J is the current density (in Amperes per square meter) flowing through the surface and ρ is the charge density (in Coulombs per cubic meter) at each point in the volume.
From the divergence theorem, we can convert this relationship from integral form to differential form:
[edit] Ampère's Circuital Law prior to Maxwell's correction
| André-Marie Ampère | |
|---|---|
| Born | January 20, 1775 |
| Died | June 10, 1836 (aged 61) Marseille,France |
| Occupation | Physicist |
In its original form, Ampère's Law (SI units) relates the magnetic field H to its source, the current density J:
Again, we can convert to differential form, this time using Stokes' theorem:
[edit] Inconsistency between Ampère's Circuital Law and the Law of Conservation of Charge
If we take the divergence of both sides of Ampère's Circuital Law, we find
The divergence of the curl of any vector field – in this case, the magnetic field H – is always equal to zero:
Combining these two equations implies that
From the law of conservation of charge, we know that
Hence, as in the case of Kirchhoff's current law, Ampère's circuital law would appear only to hold in situations involving constant charge density. This would rule out the situation that occurs in the plates of a charging or a discharging capacitor.
[edit] Maxwell's correction to Ampère's Circuital Law
To understand Maxwell's correction to Ampère's Circuital Law, we need to look at another of Maxwell's Equations, namely, Gauss's Law (SI units) in integral form:
Again, using the divergence theorem, we can convert this equation to differential form:
Taking the derivative with respect to time of both sides, we find:
Reversing the order of differentiation on the left-hand side, we obtain
This last result, along with Ampère's Circuital Law and the conservation of charge equation, suggests that there are actually two sources of the magnetic field: the current density J, as Ampère had already established, and the so-called displacement current:
So the corrected form of Ampère's Circuital Law, which Maxwell discovered, becomes:
[edit] Maxwell - First to propose that light is an electromagnetic wave
In his 1864 paper entitled A Dynamical Theory of the Electromagnetic Field, Maxwell utilized the correction to Ampère's Circuital Law that he had made in part III of his 1861 paper On Physical Lines of Force. In PART VI of his 1864 paper which is entitled 'ELECTROMAGNETIC THEORY OF LIGHT' [1] (page 497 of the article and page 9 of the pdf link), Maxwell combined displacement current with some of the other equations of electromagnetism and he obtained a wave equation with a speed equal to the speed of light. He commented,
The agreement of the results seems to show that light and magnetism are affections of the same substance, and that light is an electromagnetic disturbance propagated through the field according to electromagnetic laws.
(see [2], page 499 of the article and page 1 of the pdf link)
Maxwell's derivation of the electromagnetic wave equation has been replaced in modern physics by a much less cumbersome method involving combining the corrected version of Ampère's Circuital Law with Faraday's law of electromagnetic induction.
To obtain the electromagnetic wave equation in a vacuum using the modern method, we begin with the modern 'Heaviside' form of Maxwell's equations. Using (SI units) in a vacuum, these equations are
If we take the curl of the curl equations we obtain
If we note the vector identity
where 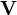 is any vector function of space, we recover the wave equations
is any vector function of space, we recover the wave equations
where
 meters per second
meters per second
is the speed of light in free space.
[edit] Covariant form of the homogeneous wave equation
These relativistic equations can be written in covariant form as
where the electromagnetic four-potential is
with the Lorenz gauge
 .
.
Here
 is the d'Alembertian operator. The square box is not a typographical error; it is the correct symbol for this operator.
is the d'Alembertian operator. The square box is not a typographical error; it is the correct symbol for this operator.
[edit] Homogeneous wave equation in curved spacetime
The electromagnetic wave equation is modified in two ways, the derivative is replaced with the covariant derivative and a new term that depends on the curvature appears.
where
is the Ricci curvature tensor and the semicolon indicates covariant differentiation.
We have assumed the generalization of the Lorenz gauge in curved spacetime
 .
.
[edit] Inhomogeneous electromagnetic wave equation
Localized time-varying charge and current densities can act as sources of electromagnetic waves in a vacuum. Maxwell's equations can be written in the form of a wave equation with sources. The addition of sources to the wave equations makes the partial differential equations inhomogeneous.
[edit] Solutions to the homogeneous electromagnetic wave equation
The general solution to the electromagnetic wave equation is a linear superposition of waves of the form
and
for virtually any well-behaved function g of dimensionless argument φ, where
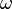 is the angular frequency (in radians per second), and
is the angular frequency (in radians per second), and is the wave vector (in radians per meter).
is the wave vector (in radians per meter).
Although the function g can be and often is a monochromatic sine wave, it does not have to be sinusoidal, or even periodic. In practice, g cannot have infinite periodicity because any real electromagnetic wave must always have a finite extent in time and space. As a result, and based on the theory of Fourier decomposition, a real wave must consist of the superposition of an infinite set of sinusoidal frequencies.
In addition, for a valid solution, the wave vector and the angular frequency are not independent; they must adhere to the dispersion relation:
where k is the wavenumber and λ is the wavelength.
[edit] Monochromatic, sinusoidal steady-state
The simplest set of solutions to the wave equation result from assuming sinusoidal waveforms of a single frequency in separable form:
where
 is the imaginary unit,
is the imaginary unit, is the angular frequency in radians per second,
is the angular frequency in radians per second, is the frequency in hertz, and
is the frequency in hertz, and is Euler's formula.
is Euler's formula.
[edit] Plane wave solutions
Consider a plane defined by a unit normal vector
 .
.
Then planar traveling wave solutions of the wave equations are
and
where
 is the position vector (in meters).
is the position vector (in meters).
These solutions represent planar waves traveling in the direction of the normal vector 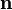 . If we define the z direction as the direction of
. If we define the z direction as the direction of 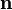 and the x direction as the direction of
and the x direction as the direction of 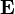 , then by Faraday's Law the magnetic field lies in the y direction and is related to the electric field by the relation
, then by Faraday's Law the magnetic field lies in the y direction and is related to the electric field by the relation
 .
.
Because the divergence of the electric and magnetic fields are zero, there are no fields in the direction of propagation.
This solution is the linearly polarized solution of the wave equations. There are also circularly polarized solutions in which the fields rotate about the normal vector.
[edit] Spectral decomposition
Because of the linearity of Maxwell's equations in a vacuum, solutions can be decomposed into a superposition of sinusoids. This is the basis for the Fourier transform method for the solution of differential equations. The sinusoidal solution to the electromagnetic wave equation takes the form
and
where
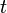 is time (in seconds),
is time (in seconds), is the angular frequency (in radians per second),
is the angular frequency (in radians per second), is the wave vector (in radians per meter), and
is the wave vector (in radians per meter), and is the phase angle (in radians).
is the phase angle (in radians).
The wave vector is related to the angular frequency by
where k is the wavenumber and λ is the wavelength.
The Electromagnetic spectrum is a plot of the field magnitudes (or energies) as a function of wavelength.
[edit] Other solutions
Spherically symmetric and cylindrically symmetric analytic solutions to the electromagnetic wave equations are also possible.