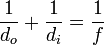Curved mirror

From Wikipedia, the free encyclopedia

Jump to: navigation, search
Reflections in a spherical convex mirror. The photographer is seen at top right

A curved mirror is a mirror with a curved reflective surface, which may be either convex (bulging outward) or concave (bulging inward). Most curved mirrors have surfaces that are shaped like part of a sphere, but other shapes are sometimes used in optical devices. The most common non-spherical type are parabolic reflectors.

Contents

  • 1 Convex mirror
    • 1.1 Image
    • 1.2 Ray diagram
  • 2 Concave mirrors
    • 2.1 Image
  • 3 Mirror shape
  • 4 Mathematical treatment of spherical mirrors
  • 5 Mirror equation and magnification
  • 6 External links

[edit] Convex mirror

A convex mirror diagram showing the focus, focal Length, centre of curvature, principal axis, etc

A convex mirror, or diverging mirror, is a curved mirror in which the reflective surface bulges toward the light source. Such mirrors always form a virtual image, since the focus F and the centre of curvature 2F are both imaginary points "inside" the mirror, which cannot be reached.

A collimated (parallel) beam of light diverges (spreads out) after reflection from a convex mirror, since the normal to the surface differs with each spot on the mirror.

[edit] Image

The image is always virtual (rays haven't actually passed though the image), diminished (smaller), and upright . These features make convex mirrors very useful: everything appears smaller in the mirror, so they cover a wider field of view than a normal plane mirror does as the image is "compressed". The passenger-side mirror on a car is typically a convex mirror. In some countries, these are labelled with the safety warning "Objects in mirror are closer than they appear", to warn the driver of the convex mirror's distorting effects on distance perception.

[edit] Ray diagram

[edit] Concave mirrors

A concave mirror diagram showing the focus, focal Length, centre of curviture, principal axis, etc.

A concave mirror, or converging mirror, has a reflecting surface that bulges inward (away from the incident light). Unlike convex mirrors, concave mirrors show different types of image depending on the distance between the object and the mirror itself.

These mirrors are called "converging" because they tend to collect light that falls on them, refocusing parallel incoming rays toward a focus. This is because the light is reflected at different angles, since the normal to the surface differs with each spot on the mirror.

[edit] Image

This sculpture has both convex and concave reflective surfaces.

Note: S here stands for distance between object and mirror.


[edit] Mirror shape

Most curved mirrors have a spherical profile. These are the simplest to make, and it is the best shape for general-purpose use. Spherical mirrors, however, suffer from spherical aberration. Parallel rays reflected from such mirrors do not focus to a single point. For parallel rays, such as those coming from a very distant object, a parabolic reflector can do a better job. Such a mirror can focus incoming parallel rays to a much smaller spot than a spherical mirror can.

See also: Toroidal reflector

[edit] Mathematical treatment of spherical mirrors

The mathematical treatment is done under the paraxial approximation, meaning that the under first approximation a spherical mirror is a parabolic reflector. The ray matrix of a spherical mirror is shown here for the concave reflecting surface of a spherical mirror. The C element of the matrix is -\frac{1}{f}, where f is the focal point of the optical device.

Boxes 1 and 3 feature summing the angles of a triangle and comparing to π radians (or 180°). Box 2 shows the Maclaurin series of \arccos\left(-\frac{r}{R}\right) up to order 1. The derivations of the ray matrices of a convex spherical mirror and a thin lens are very similar.

[edit] Mirror equation and magnification

The mirror equation relates the object distance (do) and image distances (di) to the focal length (f).

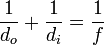
\frac{1}{d_o}+ \frac{1}{d_i} = \frac{1}{f}

The magnification of a mirror is defined as the height of the image divided by the height of the object.

m = - \frac{d_i}{d_o}

The negative sign in front of this fraction is used as a convention. Simply put, using the formula above, if the magnification is positive, the image is upright. If the magnification is negative, the image is inverted (upside down).

Consider a concave mirror, with a radius of curvature of 30.0 cm. A 10.0 cm tall object is placed 18.0 cm in front of the mirror. A ray drawn from the top of the object (10.0 cm above the principal axis) to the surface vertex (where the principal axis meets the mirror, or the center of the mirror) will form an angle with the principal axis. The ray will be reflected by the mirror below the principal axis at an angle equal to the angle of the incident ray. Remember the angle of incidence equals the angle of reflection.

A second ray can be drawn from the top of the object passing through the focal point and relecting off the mirror at a point somewhere below the principal axis. As a rule, any incident ray passing through the focal point will be reflected from the mirror as a ray parallel to the principal axis. The point at which these two reflected rays meet is the image point (the location of the image).

The height of the image hi and the height of the object ho are different in magnitude, but can be considered similar due to the two right triangles formed when drawing the two rays previously mentioned. As such, the distance to the object do and the distance to the image di are also similar.

\frac{h_o}{h_i}= \frac{d_o}{d_i}

This equation can be re-written as you refer to the drawing:

\frac{h_o}{h_i}= \frac{d_o - f}{f}

Divide both sides by do and rearrange to obtain the mirror equation:

\frac{1}{d_o}+ \frac{1}{d_i} = \frac{1}{f}