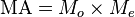Magnification

From Wikipedia, the free encyclopedia

Jump to: navigation, search

For the 2001 album of progressive rock band Yes, see Magnification (album).

Magnification is the process of enlarging something only in appearance, not in physical size. Magnification is also a number describing by which factor an object was magnified. When this number is less than one it refers to a reduction in size, sometimes called minification.

Typically magnification is related to scaling up visuals or images to be able to see more detail, increasing resolution, using optics, printing techniques, or digital processing. In all cases, the magnification of the image does not change the perspective of the image.

1 Magnification as a number (optical magnification)
- 1.1 Calculating the magnification of optical systems
- 1.2 Measurement of telescope magnification
2 Other uses
3 See also

[edit] Magnification as a number (optical magnification)

Optical magnification is the ratio between the apparent size of an object (or its size in an image) and its true size, and thus it is a dimensionless number.

Linear or transverse magnification — For real images, such as images projected on a screen, size means a linear dimension (measured, for example, in millimeters or inches).

Angular magnification — For optical instruments with an eyepiece, the linear dimension of the image seen in the eyepiece (virtual image in infinite distance) cannot be given, thus size means the angle subtended by the object at the focal point (angular size). Strictly speaking, one should take the tangent of that angle (in practice, this makes a difference only if the angle is larger than a few degrees). Thus, angular magnification is defined as

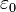$\mathrm{MA}=\frac{\tan \varepsilon}{\tan \varepsilon_0}$ ,

where ${\varepsilon_0}$ is the angle subtended by the object at the front focal point of the objective and ${\varepsilon}$ is the angle subtended by the image at the rear focal point of the eyepiece.

Example: The angular size of the full moon is 0.5°, in binoculars with 10x magnification it appears to subtend an angle of 5°, which is roughly 1/10th of the field of view of typical eyepieces.

By convention, for magnifying glasses and optical microscopes, where the size of the object is a linear dimension and the apparent size is an angle, the magnification is the ratio between the apparent (angular) size as seen in the eyepiece and the angular size of the object when placed at the conventional closest distance of distinct vision of 25 cm from the eye.

Optical magnification is sometimes referred to as "power" (for example "10× power"), although this can lead to confusion with optical power.

[edit] Calculating the magnification of optical systems

Single lens: The linear magnification of a thin lens is

$M = {f \over f-S}$

where f is the focal length and S is the distance from the lens to the object. Note that for real images, M is negative and the image is inverted. For virtual images, M is positive and the image is upright. Additionally, this can be written as the following, where di is the image distance and do is the object distance:

$M = -{di \over do}$

Note again that a negative magnification implies an inverted image.

Telescope: The linear magnification is given by

$M= {f_e \over f_o}$

where

f o

is the focal length of the objective lens and

f e

is the focal length of the eyepiece. The angular magnification is given by

$\mathrm{MA}= {f_o \over f_e}$

Magnifying glass: The angular magnification of a magnifying glass depends on how the glass and the object are held, relative to the eye. If the lens is held such that its front focal point is on the object being viewed, the relaxed eye can view the image with angular magnification

$\mathrm{MA}={25\ \mathrm{cm}\over f}\quad.$

If instead the lens is held very close to the eye, and the object is placed close to the lens, a larger angular magnification can be obtained, approaching

$\mathrm{MA}={25\ \mathrm{cm}\over f}+1\quad .$

Here,

f

is the focal length of the lens in centimeters. The constant 25 cm is an estimate of the "near point" distance of the eye—the closest distance at which the eye can focus.

Microscope: The angular magnification is given by

$\mathrm{MA}=M_o \times M_e$

where

M o

is the magnification of the objective and

M e

the magnification of the eyepiece. The magnification of the objective depends on its focal length

f o

and on the distance

d

between objective back focal plane and the focal plane of the eyepiece (called the tube length):

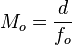$M_o={d \over f_o}$ .

The magnification of the eyepiece depends upon its focal length

f e

and can be calculated by the same equation as that of a magnifying glass (above).

Note that both astronomical telescopes as well as simple microscopes produce an inverted image, thus the equation for the magnification of a telescope or microscope is often given with a minus sign.

[edit] Measurement of telescope magnification

Measuring the actual angular magnification of a telescope is difficult, but it is possible to use the reciprocal relationship between the linear magnification and the angular magnification, since the linear magnification is constant for all objects.

The telescope is focussed correctly for viewing objects at the distance for which the angular magnification is to be determined and then the object glass is used as an object the image of which is known as the Ramsden disc. The diameter of this may be measured using an instrument known as a Ramsden dynamometer which consists of a Ramsden eyepiece with micrometer cross hairs in the back focal plane. This is mounted in front of the telescope eyepiece and used to measure the diameter of the Ramsden disc. This will be much smaller than the object glass diameter, which gives the linear magnification (actually a reduction), the angular magnification can be determined from

MA = 1 / M = D Objective / D Ramsden

[edit] Other uses