Centrifugal force

From Wikipedia, the free encyclopedia

Jump to: navigation, search

Centrifugal force (from Latin centrum "centre" and fugere "to flee") is a term which may refer to two different forces which are related to rotation. Both of them are oriented away from the axis of rotation, but the object on which they are exerted differs.

	Reactive force	Pseudo force
Reference frame	Any	Any rotating system
Exerted by	Bodies moving in circular arcs	N/A
Exerted upon	The object imposing circular motion	All bodies
Direction	Away from the axis of rotation

A real or "reactive" centrifugal force occurs in reaction to a centripetal acceleration acting on a mass. This centrifugal force is equal in magnitude to the centripetal force, directed away from the center of rotation, and is exerted by the rotating object upon the object which imposes the centripetal acceleration in accordance with Newton's Third Law of Motion. Although this sense was used by Isaac Newton,^[1] it is only occasionally used in modern discussions.^[2]^[3]^[4]^[5]

A pseudo or "fictitious" centrifugal force appears when a rotating reference frame is used for analysis. The (true) frame acceleration is substituted by a (fictitious) centrifugal force that is exerted on all objects, and directed away from the axis of rotation.

Both of the above can be easily observed in action for a passenger riding in a car. If a car swerves around a corner, a passenger's body seems to move towards the outer edge of the car and then pushes against the door.

In the reference frame that is rotating together with the car (a model which those inside the car will often find natural), it looks as if a force is pushing the passenger away from the center of the bend. This is a fictitious force--not an actual force exerted by any other object. The illusion occurs when the reference frame is the car, because that ignores the car's acceleration. A number of physicists treat it much as if it were a real force, as they find that it makes calculations simpler and gives correct results.

However, the force with which the passenger pushes against the door is real. That force is called a reaction force because it results from passive interaction with the car which actively pushes against the body. As it is directed outward, it is a centrifugal force. Note that this real centrifugal force does not appear until the person touches the body of the car (ignoring any force exerted by the seat on the person's body, etc). The car also exerts an equal but opposite force on the person, called "centripetal force".

1 Reactive centrifugal force
2 Rotating reference frames
3 Fictitious forces
- 3.1 Potential energy
4 Confusion and misconceptions
5 Applications
6 See also
7 References
8 Notes

[edit] Reactive centrifugal force

When viewed from an inertial frame of reference, the application of Newton's laws of motion is simple. The passenger's inertia resists acceleration, keeping the passenger moving with constant speed and direction as the car begins to turn. From this point of view, the passenger does not gravitate toward the outside of the path which the car follows; instead, the car's path curves to meet the passenger.

Once the car contacts the passenger, it then applies a sideways force to accelerate him or her around the turn with the car. This force is called a centripetal ("center seeking") force because its vector changes direction to continue to point toward the center of the car's arc as the car traverses it.

If the car is acting upon the passenger, then the passenger must be acting upon the car with an equal and opposite force. Being opposite, this reaction force is directed away from the center, therefore centrifugal.^[6] It is critical to realize that this centrifugal force acts upon the car, not the passenger.

The centrifugal reaction force with which the passenger pushes back against the door of the car is given by:

$\mathbf{F}_\mathrm{centrifugal} \,$	$= - m \mathbf{a}_\mathrm{centripetal} \,$
	$= m \omega^2 \mathbf{r}_\perp \,$

where $m$ is the mass of the rotating object, $ω$ the rotational speed (in radians per unit time), and $r$ the radius of the rotation.

The reactive centrifugal force^[7] is a real force, but the term is rarely used in modern discussions.^[8]^[9]

[edit] Rotating reference frames

In the classical approach, the inertial frame remains the true reference for the laws of mechanics and analysis. When using a rotating reference frame, the laws of physics are mapped from the most convenient inertial frame to that rotating frame. Assuming a constant rotation speed, this is achieved by adding to every object two coordinate accelerations which correct for the rotation of the coordinate axes.

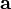$\mathbf{a}_\mathrm{rot}\,$	$=\mathbf{a} - 2\mathbf{\omega \times v} - \mathbf{\omega \times (\omega \times r)} \,$
	$=\mathbf{a + a_\mathrm{Coriolis} + a_\mathrm{centrifugal}} \,$

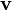where $\mathbf{a}_\mathrm{rot}\,$ is the acceleration relative to the rotating frame, $\mathbf{a}\,$ is the acceleration relative to the inertial frame, $\mathbf{\omega}\,$ is the angular velocity vector describing the rotation of the reference frame, $\mathbf{v}\,$ is the velocity of the body relative to the rotating frame, and $\mathbf{r}\,$ is a vector from an arbitrary point on the rotation axis to the body. A derivation can be found in the article fictitious force.

The last term is the centrifugal acceleration, so we have:

$\mathbf{a}_\textrm{centrifugal} = - \mathbf{\omega \times (\omega \times r)} = \omega^2 \mathbf{r}_\perp$

where $\mathbf{r_\perp}$ is the component of $\mathbf{r}\,$ perpendicular to the axis of rotation.

[edit] Fictitious forces

Main article: Fictitious force

An alternative way of dealing with a rotating frame of reference is to make Newton's laws of motion artificially valid by adding pseudo forces to be the cause of the above acceleration terms. In particular, the centrifugal acceleration is added to the motion of every object, and attributed to a centrifugal force, given by:

$\mathbf{F}_\mathrm{centrifugal} \,$	$= m \mathbf{a}_\mathrm{centrifugal} \,$
	$=m \omega^2 \mathbf{r}_\perp \,$

where $m\,$ is the mass of the object.

This pseudo or fictitious[1] centrifugal force is a sufficient correction to Newton's second law only if the body is stationary in the rotating frame. For bodies that move with respect to the rotating frame it must be supplemented with a second pseudo force, the "Coriolis force":

$\mathbf{F}_\mathrm{coriolis} = -2m \mathbf{\omega \times v} = -2m \omega^2 \mathbf{r}_\perp$

For example, a body that is stationary relative to the non-rotating frame, will be rotating when viewed from the rotating frame. The centripetal force of 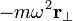$-m \omega^2 \mathbf{r}_\perp$ required to account for this apparent rotation is the sum of the centrifugal pseudo force ( $m \omega^2 \mathbf{r}_\perp$ ) and the Coriolis force ( $-2m \mathbf{\omega \times v} = -2m \omega^2 \mathbf{r}_\perp$ ). Since this centripetal force includes contributions from only pseudo forces, it has no reactive counterpart.

[edit] Potential energy

The interface of two immiscible liquids rotating around a vertical axis is an upward-opening circular paraboloid.

The fictitious centrifugal force can be described by a potential energy of the form

$E_p = -\frac{1}{2} m \omega^2 r_\perp^2$

This is useful, for example, in calculating the form of the water surface $h(r)\,$ in a rotating bucket: requiring the potential energy per unit mass on the surface $gh(r) - \frac{1}{2}\omega^2 r^2\,$ to be constant, we obtain the parabolic form $h(r) = \frac{\omega^2}{2g}r^2 + C$ (where $C$ is a constant).

Similarly, the potential energy of the centrifugal force is often used in the calculation of the height of the tides on the Earth (where the centrifugal force is included to account for the rotation of the Earth around the Earth-Moon center of mass).

The principle of operation of the centrifuge also can be simply understood in terms of this expression for the potential energy, which shows that it is favorable energetically when the volume far from the axis of rotation is occupied by the heavier substance.

The coriolis force has no equivalent potential, as it acts perpendicular to the velocity vector and hence rotates the direction of motion, but does not change the energy of a body.

[edit] Confusion and misconceptions

Centrifugal force can be a confusing term because it is used (or misused) in more than one instance, and because sloppy labelling can obscure which forces are acting upon which objects in a system. When diagramming forces in a system, one must describe each object separately, attaching only those forces acting upon it (not forces that it exerts upon other objects).

One can avoid dealing with pseudo forces entirely by analyzing systems using inertial frames of reference for the physics; and when convenient, one simply maps to a rotating frame without forgetting about the frame rotation, as shown above. Such is standard practice in mechanics textbooks.

Because rotating frames are not vital for understanding mechanics, they are often not discussed in science education. Therefore teachers who need to impress on their students that centrifugal forces have no place in their calculations often do not have occasion to give a matching emphasis to the fact that a centrifugal force does occur in a rotating frame. As a result, even students who master the physics curriculum may leave school with the false impression that it is never scientifically valid to speak about centrifugal forces.^{[neutrality disputed]} Nevertheless, many popular discussions of forces do use the term "centrifugal", without pointing out that it is fictitious, and assume the reader is knowledgeable of the true inertial character of the force, leading to misconceptions and bad use of the term.

[edit] Applications

A centrifugal governor regulates the speed of an engine by using spinning masses that respond to centrifugal force generated by the engine. If the engine increases in speed, the masses move and trigger a cut in the throttle.
A centrifugal clutch is used in small engine powered devices such as chain saws, go-karts and model helicopters. It allows the engine to start and idle without driving the device but automatically and smoothly engages the drive as the engine speed rises.
Centrifugal forces can be used to generate artificial gravity. Proposals have been made to have gravity generated in space stations designed to rotate. The Mars Gravity Biosatellite will study the effects of Mars level gravity on mice with simulated gravity from centrifugal force.
Centrifuges are used in science and industry to separate substances by their relative masses.
Some amusement park rides make use of centrifugal forces. For instance, a Gravitron’s spin forces riders against a wall and allows riders to be elevated above the machine’s floor in defiance of Earth’s gravity.
Spin casting and centrifugal casting are production methods that uses centrifugal force to disperse liquid metal or plastic throughout the negative space of a mold.