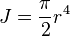Torsion (mechanics)

From Wikipedia, the free encyclopedia

Jump to: navigation, search

Look up torsion in Wiktionary, the free dictionary.

Wikibooks has a book on the topic of

Solid Mechanics

In solid mechanics, torsion is the twisting of an object due to an applied torque. In circular sections, the resultant shearing stress is perpendicular to the radius.

The shear stress at a point on a shaft is:

$\tau_{\phi_{z}} = {T r \over J}$

Note that the highest shear stress is at the point where the radius is maximum, the surface of the shaft. High stresses at the surface may be compounded by stress concentrations such as rough spots. Thus, shafts for use in high torsion are polished to a fine surface finish to reduce the maximum stress in the shaft and increase its service life.

The angle of twist can be found by using:

$\phi_{} = {T L \over JG}$

Where:

r is the distance from the center of rotation
Φ is the angle of twist in radians.
T is the torque (N·m or ft·lb_f).
L is the length of the object the torque is being applied to or over.
G is the shear modulus or more commonly the modulus of rigidity and is usually given in gigapascals (GPa), lb_f/in² (psi), or lb_f/ft².
J is the torsional constant for the section . It is identical to the polar moment of inertia for a round shaft or concentric tube only. For other shapes J must be determined by other means. For solid shafts the membrane analogy is useful, and for thin walled tubes of arbitrary shape the shear flow approximation is fairly good, if the section is not re-entrant. For thick walled tubes of arbitrary shape there is no simple solution, FEA may be the best method.

[edit] Polar moment of inertia

Main article: Polar moment of inertia

The polar moment of inertia for a solid shaft is:

$J = {\pi \over 2} r^4$

Where r is the radius of the object.

The polar moment of inertia for a pipe is:

$J = {\pi \over 2} (r_{o}^4 - r_{i}^4)$

Where the o and i subscripts stand for the outer and inner radius of the pipe.

For a thin cylinder

J = 2π R³ t

Where R is the average of the outer and inner radius and t is the wall thickness.

[edit] Failure mode

The shear stress in the shaft may be resolved into principal stresses via Mohr's circle. If the shaft is loaded only in torsion then one of the principal stresses will be in tension and the other in compression. These stresses are oriented at a 45 degree helical angle around the shaft. If the shaft is made of brittle material then the shaft will fail by a crack initiating at the surface and propagating through to the core of the shaft fracturing in a 45 degree angle helical shape. This is often demonstrated by twisting a piece of blackboard chalk between one's fingers.