Scale relativity
From Wikipedia, the free encyclopedia
Scale relativity is a theory of physics initially developed by Laurent Nottale, working at the french observatory of Meudon, near Paris, which extends special and general relativity with a new formulation of scale invariance preserving a reference length, postulated to be the Planck length, which becomes invariant under zoom. This requires abandoning the hypothesis of differentiability for space-time, instead suggesting that space-time has a fractal structure. The quantum/classical transition is replaced with a fractal/non-fractal transition, specifically a divergence in the length of quantum paths at short scale.
Contents
|
[edit] Scale Relativity principle
The scale relativity extends to scales the reasoning made by Einstein on speeds in special relativity: just like a constant speed 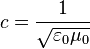 in Maxwell's equations, which does not appear to depend on the speed of the observer, suggests that the law of combination of speeds must preserve this invariant, similalry, the appearance of a constant length
in Maxwell's equations, which does not appear to depend on the speed of the observer, suggests that the law of combination of speeds must preserve this invariant, similalry, the appearance of a constant length  in Schrödinger's equation suggests that the law of combination of scales must preserve this invariant. In other words, just like c is a physical speed limit,
in Schrödinger's equation suggests that the law of combination of scales must preserve this invariant. In other words, just like c is a physical speed limit, 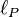 is a physical length limit.
is a physical length limit.
[edit] Predictions and retrodictions
Scale relativity made a number of true predictions, as well as a number of retrodictions, both in cosmology and at small scale, including:
- Prediction of the location of exoplanets[1]
- Explanation of some observed large-scale structures [2]
- Relation between mass and charge of the electron [3]
