Quantum state
From Wikipedia, the free encyclopedia
| The introduction to this article provides insufficient context for those unfamiliar with the subject matter. Please help improve the introduction to meet Wikipedia's layout standards. You can discuss the issue on the talk page. |
In quantum mechanics, the quantum state of a system is a set of numbers that fully describe a quantum system. Since quantum theory is non-deterministic, these numbers only relate to the likely outcome of measuring a parameter of the system, such as its energy or angular momentum (see Measurement in quantum mechanics). These numbers are called the quantum numbers of the system.
In classical mechanics, a particle would be described in terms of its position and momentum. In quantum mechanics however, the position and momentum of a particle cannot be exactly measured, so instead, particles are described by a set of quantum numbers that are specific to the system being described. For example, in the case of a single particle in a one dimensional box, the state of a particle can be defined by a single quantum number related to the energy of this particle.
All experimental predictions are based on the quantum state of the system and the quantum operations acting on the state. A fully specified quantum state can be described by a state vector, a wave function, or a complete set of quantum numbers for a specific system. A partially known quantum state, such as an ensemble with some quantum numbers fixed, can be described by a density matrix.
Contents
|
[edit] Conceptual description
[edit] The state of a physical system
The state of a physical system is a complete description of the parameters of the experiment. To understand this rather abstract notion, it is useful to first explore it in an example from classical mechanics.
Consider an experiment with a (non-quantum) particle of mass m = 1 which moves freely, and without friction, in one spatial direction.
We start the experiment at time t = 0 by pushing the particle with some speed into some direction. Doing this, we determine the initial position q and the initial momentum p of the particle. These initial conditions are what characterizes the state σ of the system, formally denoted as σ = (p,q). We say that we prepare the state of the system by fixing its initial conditions.
At a later time t > 0, we conduct measurements on the particle. The measurements we can perform on this simple system are essentially its position Q(t) at time t, its momentum P(t), and combinations of these. Here P(t) and Q(t) refer to the measurable quantities (observables) of the system as such, not the specific results they produce in a certain run of the experiment.
However, knowing the state σ of the system, we can compute the value of the observables in the specific state, i.e., the results that our measurements will produce, depending on p and q. We denote these values as  and
and  . In our simple example, it is well known that the particle moves with constant velocity; therefore,
. In our simple example, it is well known that the particle moves with constant velocity; therefore,

Now suppose that we start the particle with a random initial position and momentum. (For argument's sake, we may suppose that the particle is pushed away at t = 0 by some apparatus which is controlled by a random number generator.) The state σ of the system is now not described by two numbers p and q, but rather by two probability distributions. The observables P(t) and Q(t) will produce random results now; they become random variables, and their values in a single measurement cannot be predicted. However, if we repeat the experiment sufficiently often, always preparing the same state σ, we can predict the expectation value of the observables (their statistical mean) in the state σ. The expectation value of P(t) is again denoted by  , etc.
, etc.
These "statistical" states of the system are called mixed states, as opposed to the pure states σ = (p,q) discussed further above. Abstractly, mixed states arise as a statistical mixture of pure states.
[edit] Quantum states
In quantum systems, the conceptual distinction between observables and states persists just as described above. The state σ of the system is fixed by the way the physicist prepares his experiment (e.g., how he adjusts his particle source). As above, there is a distinction between pure states and mixed states, the latter being statistical mixtures of the former. However, some important differences arise in comparison with classical mechanics.
In quantum theory, even pure states show statistical behaviour. Regardless of how carefully we prepare the state ρ of the system, measurement results are not repeatable in general, and we must understand the expectation value  of an observable A as a statistical mean. It is this mean that is predicted by physical theories.
of an observable A as a statistical mean. It is this mean that is predicted by physical theories.
For any fixed observable A, it is generally possible to prepare a pure state σA such that A has a fixed value in this state: If we repeat the experiment several times, each time measuring A, we will always obtain the same measurement result, without any random behaviour. Such pure states σA are called eigenstates of A.
However, it is generally impossible to prepare a simultaneous eigenstate for all observables. For example, we cannot prepare a state such that both the position measurement Q(t) and the momentum measurement P(t) (at the same time t) produce "sharp" results; at least one of them will exhibit random behaviour. This is the content of the Heisenberg uncertainty relation.
Moreover, in contrast to classical mechanics, it is unavoidable that performing a measurement on the system changes its state. More precisely: After measuring an observable A, the system will be in an eigenstate of A. This expresses a kind of logical consistency: If we measure A twice in the same run of the experiment, the measurements being directly consecutive in time, then they will produce the same results. This has some strange consequences however:
Consider two observables, A and B, where A corresponds to a measurement earlier in time than B. Suppose that the system is in an eigenstate of B. If we measure only B, we will not notice statistical behaviour. If we measure first A and then B in the same run of the experiment, the system will transfer to an eigenstate of A after the first measurement, and we will generally notice that the results of B are statistical. Thus, quantum mechanical measurements influence one another, and it is important in which order they are performed.
Another feature of quantum states becomes relevant if we consider a physical system that consists of multiple subsystems; for example, an experiment with two particles rather than one. Quantum physics allows for certain states, called entangled states, that show certain statistical correlations between measurements on the two particles which cannot be explained by classical theory. For details, see entanglement. These entangled states lead to experimentally testable properties (Bell's theorem) that allow to distinguish between quantum theory and alternative classical (non-quantum) models.
[edit] Schrödinger picture vs. Heisenberg picture
In the discussion above, we have taken the observables P(t), Q(t) to be dependent on time, while the state σ was fixed once at the beginning of the experiment. This approach is called the Heisenberg picture. One can, equivalently, treat the observables as fixed, while the state of the system depends on time; that is known as the Schrödinger picture. Conceptually (and mathematically), both approaches are equivalent; choosing one of them is a matter of convention.
Both viewpoints are used in quantum theory. While non-relativistic quantum mechanics is usually formulated in terms of the Schrödinger picture, the Heisenberg picture is often preferred in a relativistic context, that is, for quantum field theory.
[edit] Formalism in quantum physics
[edit] Bra-ket notation
Paul Dirac invented a powerful and intuitive notation to describe quantum states, known as bra-ket notation. For instance, one can refer to an |excited atom> or to  for a spin-up particle, hiding the underlying complexity of the mathematical description, which is revealed when the state is projected onto a coordinate basis. For instance, the simple notation |1s> describes the first hydrogen atom bound state, but becomes a complicated function in terms of Laguerre polynomials and spherical harmonics when projected onto the basis of position vectors |r>. The resulting expression Ψ(r)=<r|1s>, which is known as the wave function, is a special representation of the quantum state, namely, its projection into position space. Other representations, such as projection into momentum space, are possible. The various representations are simply different expressions of a single physical quantum state.
for a spin-up particle, hiding the underlying complexity of the mathematical description, which is revealed when the state is projected onto a coordinate basis. For instance, the simple notation |1s> describes the first hydrogen atom bound state, but becomes a complicated function in terms of Laguerre polynomials and spherical harmonics when projected onto the basis of position vectors |r>. The resulting expression Ψ(r)=<r|1s>, which is known as the wave function, is a special representation of the quantum state, namely, its projection into position space. Other representations, such as projection into momentum space, are possible. The various representations are simply different expressions of a single physical quantum state.
[edit] Basis states
Any quantum state  can be expressed in terms of a sum of basis states (also called basis kets)
can be expressed in terms of a sum of basis states (also called basis kets) 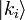 in the form
in the form
where ci are the coefficients representing the probability amplitude, such that the absolute square of the probability amplitude,  is the probability of a measurement in terms of the basis states yielding the state
is the probability of a measurement in terms of the basis states yielding the state 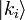 . The normalization condition mandates that the total sum of probabilities is equal to one,
. The normalization condition mandates that the total sum of probabilities is equal to one,
The simplest understanding of basis states is obtained by examining the quantum harmonic oscillator. In this system, each basis state  has an energy
has an energy  . The set of basis states can be extracted using a construction operator
. The set of basis states can be extracted using a construction operator  and a destruction operator
and a destruction operator 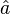 in what is called the ladder operator method.
in what is called the ladder operator method.
[edit] Superposition of states
If a quantum mechanical state  can be reached by more than one path, then
can be reached by more than one path, then  is said to be a linear superposition of states. In the case of two paths, if the states after passing through path α and path β are
is said to be a linear superposition of states. In the case of two paths, if the states after passing through path α and path β are
 and
and
then  is defined as the normalized linear sum of these two states. If the two paths are equally likely, this yields
is defined as the normalized linear sum of these two states. If the two paths are equally likely, this yields
Note that in the states 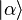 and
and  the two states
the two states  and
and  each have a probability of
each have a probability of  as obtained by the absolute square of the probability amplitudes, which are
as obtained by the absolute square of the probability amplitudes, which are  and
and  In a superposition, it is the probability amplitudes which add, and not the probabilities themselves. The pattern which results from a superposition is often called an interference pattern. In the above case,
In a superposition, it is the probability amplitudes which add, and not the probabilities themselves. The pattern which results from a superposition is often called an interference pattern. In the above case,  is said to constructively interfere, and
is said to constructively interfere, and  is said to destructively interfere.
is said to destructively interfere.
For more about superposition of states, see the double-slit experiment.
[edit] Pure and mixed states
A pure quantum state is a state which can be described by a single ket vector, or as a sum of basis states. A mixed quantum state is a statistical distribution of pure states.
The expectation value 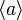 of a measurement A on a pure quantum state is given by
of a measurement A on a pure quantum state is given by
where 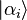 are basis kets for the operator A, and P(αi) is the probability of
are basis kets for the operator A, and P(αi) is the probability of  being measured in state
being measured in state 
In order to describe a statistical distribution of pure states, or mixed state, the density matrix (or density operator), ρ, is used. This extends quantum mechanics to quantum statistical mechanics. The density operator is defined as
where ps is the fraction of each ensemble in pure state 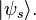 The ensemble average of a measurement A on a mixed state is given by
The ensemble average of a measurement A on a mixed state is given by
where it is important to note that two types of averaging are occurring, one being a quantum average over the basis kets of the pure states, and the other being a statistical average over the ensemble of pure states.
[edit] Mathematical formulation
For a mathematical discussion on states as functionals, see Gelfand-Naimark-Segal construction. There, the same objects are described in a C*-algebraic context.

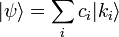




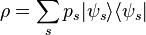
![\left [ A \right ] = \langle \overline{A} \rangle = \sum_s p_s \langle \psi_s | A | \psi_s \rangle = \sum_s \sum_i p_s a_i | \langle \alpha_i | \psi_s \rangle |^2 = tr(\rho A)](http://upload.wikimedia.org/math/b/8/e/b8e1e5cd9604946f41adbee3af5a6abf.png)