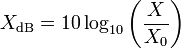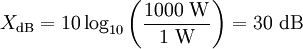Decibel

From Wikipedia, the free encyclopedia

Jump to: navigation, search

For other uses, see Decibel (disambiguation).

The decibel (dB) is a logarithmic unit of measurement that expresses the magnitude of a physical quantity (usually power) relative to a specified or implied reference level. Its logarithmic nature allows very large or very small ratios to be represented by a convenient number, in a similar manner to scientific notation. Being essentially a ratio, it is a dimensionless unit. Decibels are useful for a wide variety of measurements in acoustics, physics, electronics and other disciplines.

The decibel is not an SI unit, although the International Committee for Weights and Measures (CIPM) has recommended its inclusion in the SI system. Following the SI convention, the d is lowercase, as it represents the SI prefix deci-, and the B is capitalized, as it is an abbreviation of a name-derived unit, the bel (see below). The full name decibel follows the usual English capitalization rules for a common noun. The decibel symbol is often qualified with a suffix, which indicates which reference quantity has been assumed. For example, "dBm" indicates that the reference quantity is one milliwatt.

A decibel is one tenth of a bel (B). Devised by engineers of the Bell Telephone Laboratory to quantify the reduction in audio level over a 1 mile (approximately 1.6 km) length of standard telephone cable, the bel was originally called the transmission unit or TU, but was renamed in 1923 or 1924 in honor of the Bell System's founder and telecommunications pioneer Alexander Graham Bell. In many situations, however, the bel proved inconveniently large, so the decibel has become more common.

The definitions of the decibel and bel use base-10 logarithms. For a similar unit using natural logarithms to base e, see neper.

An increase of 3 dB corresponds to an approximate doubling of power. (In exact terms, the factor is 10^3/10, or 1.9953, about 0.24% different from exactly 2.) Since in many electrical applications power is proportional to the square of voltage, an increase of 3 dB implies an increase in voltage by a factor of approximately √2, or about 1.41. Similarly, an increase of 6 dB corresponds to approximately four times the power and twice the voltage, and so on. (In exact terms the power factor is 10^6/10, or about 3.9811, a relative error of about 0.5%.) See the formulas below for further details.

1 Definitions
- 1.1 Power
- 1.2 Amplitude, voltage and current
- 1.3 Examples
2 Merits
3 Uses
- 3.1 Acoustics
- 3.2 Electronics
- 3.3 Optics
- 3.4 Seismology
4 Common reference levels and corresponding units
- 4.1 "Absolute" and "relative" decibel measurements
- 4.2 Absolute measurements
  - 4.2.1 Electric power
  - 4.2.2 Voltage
  - 4.2.3 Acoustics
  - 4.2.4 Radio power or energy
- 4.3 Relative measurements
5 Reckoning
- 5.1 Round numbers
- 5.2 The 4 → 6 energy rule
- 5.3 The "789" rule
- 5.4 −3 dB ≈ ½ power
- 5.5 6 dB per bit
- 5.6 dB chart
  - 5.6.1 Commonly used dB values
6 See also
7 References
8 External links
- 8.1 Converters

[edit] Definitions

[edit] Power

When referring to measurements of power or intensity, a ratio can be expressed in decibels by evaluating ten times the base-10 logarithm of the ratio of the measured quantity to the reference level. Thus, X_dB is calculated using the formula:

$X_\mathrm{dB} = 10 \log_{10} \bigg(\frac{X}{X_0}\bigg) \$

where X is the actual value of the quantity being measured, X₀ is a specified or implied reference level, and then X_dB is the quantity expressed in units of decibels, relative to X₀. Which reference is used depends on convention and context (see later in this article). X and X₀ must have the same dimensions (that is, must measure the same type of quantity), and must as necessary be converted to the same units before calculating the ratio of their numerical values. The reference level itself is always at 0 dB, as shown by setting X = X₀ in the above equation. If X is greater than X₀ then X_dB is positive; if X is less than X₀ then X_dB is negative.

Rearranging the above equation gives the following formula for X in terms of X₀ and X_dB:

$X = 10^\frac{X_\mathrm{dB}}{10} X_0.$

Since a bel is equal to ten decibels, the corresponding formulae for measurement in bels (X_B) are

$X_\mathrm{B} = \log_{10} \bigg(\frac{X}{X_0}\bigg) \$

$X = 10^{X_\mathrm{B}} X_0.$

[edit] Amplitude, voltage and current

When referring to measurements of amplitude it is usual to consider the ratio of the squares of X (measured amplitude) and X₀ (reference amplitude). This is because in most applications power is proportional to the square of amplitude. Thus the following definition is used:

$X_\mathrm{dB} = 10 \log_{10} \bigg(\frac{X^2}{X_0^2}\bigg) = 20 \log_{10} \bigg(\frac{X}{X_0}\bigg)$

The formula may be rearranged to give

$X = 10^\frac{X_\mathrm{dB}}{20} X_0$

Similarly, in electrical circuits, dissipated power is typically proportional to the square of voltage or current when the impedance is held constant. Taking voltage as an example, this leads to the equation:

$V_\mathrm{dB} =20 \log_{10} \left (\frac{V}{V_0} \right ) \quad \mathrm \quad$

where V is the voltage being measured, V₀ is a specified reference voltage, and V_dB is the voltage gain expressed in decibels. A similar formula holds for current.

[edit] Examples

These examples assume that X in the formulas above measures power relative to 1 W (one watt); i.e. X₀ = 1 W.

To convert 1 kW (one kilowatt, or 1000 W) to decibels, use the formula

$X_\mathrm{dB} = 10 \log_{10} \bigg(\frac{1000\ \mathrm{W}}{1\ \mathrm{W}}\bigg) = 30\ \mathrm{dB}$

To convert 1 mW (one milliwatt, or 0.001 W) to decibels, use the formula

$X_\mathrm{dB} = 10 \log_{10} \bigg(\frac{0.001\ \mathrm{W}}{1\ \mathrm{W}}\bigg) = -30\ \mathrm{dB}$

To find the actual value of 3 dB, use the formula

$X = 10^\frac{3}{10} \times 1\ \mathrm{W} = 1.99526...\ \mathrm{W} \approx 2\ \mathrm{W}$

It will be seen that there is a 10 dB increase (decrease) for each factor 10 increase (decrease) in the ratio of X to X₀, and approximately a 3 dB increase (decrease) for every factor 2 increase (decrease).

[edit] Merits

The use of decibels has a number of merits:

The mathematical laws of exponents mean that the overall decibel gain of a multi-component system (such as consecutive amplifiers) can be calculated simply by summing the decibel gains of the individual components, rather than needing to multiply amplification factors.
A very large range of ratios can be expressed with decibel values in a range of moderate size, allowing one to clearly visualize huge changes of some quantity. (See Bode Plot and half logarithm graph.)
In acoustics, the decibel scale approximates the human perception of loudness (which is itself roughly logarithmic).

[edit] Uses

[edit] Acoustics

Main article: Sound pressure

The decibel is commonly used in acoustics to quantify sound levels relative to some 0 dB reference. The reference level is typically set at the threshold of human perception; see sound pressure.

A reason for using the decibel is that the ear is capable of detecting a very large range of sound pressures (see Examples of sound pressure and sound pressure levels). The ratio of the sound pressure that causes permanent damage from short exposure to the limit that (undamaged) ears can hear is above a million. Because the power in a sound wave is proportional to the square of the pressure, the ratio of the maximum power to the minimum power is above one (short scale) trillion. To deal with such a range, logarithmic units are useful: the log of a trillion is 12, so this ratio represents a difference of 120 dB. Since the human ear is not equally sensitive to all the frequencies of sound within the entire spectrum, noise levels at maximum human sensitivity — middle A and its higher harmonics (between 2 and 4 kHz) — are factored more heavily into sound descriptions using a process called frequency weighting.

[edit] Electronics

The decibel is used rather than arithmetic ratios or percentages because when certain types of circuits, such as amplifiers and attenuators, are connected in series, expressions of power level in decibels may be arithmetically added and subtracted. It is also common in disciplines such as audio, in which the properties of the signal are best expressed in logarithms due to the response of the human ear.

In radio electronics and telecommunications, the decibel is used to describe the ratio between two measurements of electrical power. It can also be combined with a suffix to create an absolute unit of electrical power. For example, it can be combined with "m" for "milliwatt" to produce the "dBm". Zero dBm is one milliwatt, and 1 dBm is one decibel greater than 0 dBm, or about 1.259 mW.

Decibels are used to account for the gains and losses of a signal from a transmitter to a receiver through some medium (free space, wave guides, coax, fiber optics, etc.) using a link budget.

In professional audio, a popular unit is the dBu (see below for all the units). The "u" stands for "unloaded", and was probably chosen to be similar to lowercase "v", as dBv was the older name for the same thing. It was changed to avoid confusion with dBV. This unit (dBu) is an RMS measurement of voltage which uses as its reference 0.775 V_RMS. Chosen for historical reasons, it is the voltage level at which you get 1 mW of power in a 600 ohm resistor, which used to be the standard reference impedance in almost all professional low impedance audio circuits.

The bel is used to represent noise power levels in hard drive specifications.

[edit] Optics

In an optical link, if a known amount of optical power, in dBm (referenced to 1 mW), is launched into a fibre, and the losses, in dB (decibels), of each electronic component (e.g., connectors, splices, and lengths of fibre) are known, the overall link loss may be quickly calculated by simple addition and subtraction of decibel quantities.

In spectrometry and optics, the blocking unit used to measure optical density is equivalent to −1 B. In astronomy, the apparent magnitude measures the brightness of a star logarithmically, since, just as the ear responds logarithmically to acoustic power, the eye responds logarithmically to brightness; however astronomical magnitudes reverse the sign with respect to the bel, so that the brightest stars have the lowest magnitudes, and the magnitude increases for fainter stars.

[edit] Seismology

Earthquakes were formerly measured on the Richter scale, which is expressed in bels, though they are not labeled with a unit. The more modern moment magnitude scale is designed to produce values comparable to those of the Richter scale.

[edit] Common reference levels and corresponding units

[edit] "Absolute" and "relative" decibel measurements

Although decibel measurements are always relative to a reference level, if the numerical value of that reference is explicitly and exactly stated, then the decibel measurement is called an "absolute" measurement, in the sense that the exact value of the measured quantity can be recovered using the formulas given earlier. For example, since dBm indicates power measurement relative to 1 milliwatt,

0 dBm means no change from 1 mW, in other words 0 dBm is 1 mW.
3 dBm means 3 dB greater than 1 mW. 3 dBm is 10^3/10 × 1 mW, or approximately 2 mW.
−6 dBm means 6 dB less than 1 mW. −6 dBm is 10^−6/10 × 1 mW, or approximately 250 μW (0.25 mW).

If the numerical value of the reference is not explicitly stated, as in the dB gain of an amplifier, then the decibel measurement is purely relative.

[edit] Absolute measurements

[edit] Electric power

dBm or dBmW

dB(1 mW) — power measurement relative to 1 milliwatt. X_dBm = X_dBW + 30.

dBW

dB(1 W) — similar to dBm, except the reference level is 1 watt. 0 dBW = +30 dBm; -30 dBW = 0 dBm; X_dBW = X_dBm - 30.

[edit] Voltage

Note that the decibel has a different definition when applied to voltage (as contrasted with power). See the "Definitions" section above.

A schematic showing the relationship between dBu (the voltage source) and dBm (the power dissipated as heat by the 600 Ω resistor)

dBu or dBv

dB(0.775 V_RMS) — voltage relative to 0.775 volts.^[1] Originally dBv, it was changed to dBu to avoid confusion with dBV.^{[citation needed]} The "v" comes from "volt", while "u" comes from "unloaded". dBu can be used regardless of impedance, but is derived from a 600 Ω load dissipating 0 dBm (1 mW).

dBV

dB(1 V_RMS) — voltage relative to 1 volt, regardless of impedance.^[2]

dBmV

dB(1 mV_RMS) — voltage relative to 1 millivolt, regardless of impedance. Widely used in cable television networks, where the nominal strength of a single TV signal at the receiver terminals is about 0 dBmV. Cable TV uses 75 Ω coaxial cable, so 0 dBmV corresponds to -48.75 dBm or ~13 nW.

[edit] Acoustics

dB(SPL)

dB (Sound Pressure Level) — for sound in air and other gases, relative to 20 micropascals (μPa) = 2×10⁻⁵ Pa, the quietest sound a human can hear. This is roughly the sound of a mosquito flying 3 metres away. This is often abbreviated to just "dB", which gives some the erroneous notion that "dB" is an absolute unit by itself. For sound in water and other liquids, a reference pressure of 1 μPa is used.^[3]

dB SIL

dB Sound Intensity Level — relative to 10⁻¹² W/m², which is roughly the threshold of human hearing in air.

dB SWL

dB Sound Power Level — relative to 10⁻¹² W.

dB(A), dB(B), and dB(C)

These symbols are often used to denote the use of different frequency weightings, used to approximate the human ear's response to sound, although the measurement is still in dB (SPL). Other variations that may be seen are dB_A or dBA. According to ANSI standards, the preferred usage is to write L_A = x dB, as dBA implies a reference to an "A" unit, not an A-weighting. They are still used commonly as a shorthand for A-weighted measurements, however.

[edit] Radio power or energy

dBJ

dB(J) — energy relative to 1 joule. 1 joule = 1 watt-second, so noise spectral density can be expressed in dBJ, where 0 dBJ = 0 dBW/Hz. Boltzmann's constant is -228.6 dBJ/K.

dBm

dB(mW) — power relative to 1 milliwatt.

dBμ or dBu

dB(μV/m) — electric field strength relative to 1 microvolt per metre.

dBf

dB(fW) — power relative to 1 femtowatt.

dBW

dB(W) — power relative to 1 watt.

dBk

dB(kW) — power relative to 1 kilowatt.

[edit] Relative measurements

dBd

dB(dipole) — the forward gain of an antenna compared to a half-wave dipole antenna.

dBFS or dBfs

dB(full scale) — the amplitude of a signal (usually audio) compared to the maximum which a device can handle before clipping occurs. In digital systems, 0 dBFS (peak) would equal the highest level (number) the processor is capable of representing. Measured values are usually negative, since they should be less than the maximum.

dB-Hz

dB(Hertz) — Bandwidth relative to 1 Hz. E.g., 20 dB-Hz is equal to 100 Hz. Commonly used in link budget calculations.

dBi

dB(isotropic) — the forward gain of an antenna compared to a fictitious isotropic antenna, which uniformly distributes energy in all directions.

dBiC

dB(isometric circular) — power measurement relative to a circularly polarized isometric antenna.

dBov or dBO

dB(overload) — the amplitude of a signal (usually audio) compared to the maximum which a device can handle before clipping occurs. Similar to dBFS, but also applicable to analog systems.

dBr

dB(relative) — simply a relative difference to something else, which is made apparent in context. The difference of a filter's response to nominal levels, for instance.

dBrn

dB above reference noise. See also dBrnC.

dBc

dB relative to carrier — in telecommunications, this indicates the relative levels of noise or sideband peak power, compared to the carrier power.

[edit] Reckoning

Decibels are handy for mental calculation, because adding them is easier than multiplying ratios. First, however, one has to be able to convert easily between ratios and decibels. The most obvious way is to memorize the logs of small primes, but there are a few other tricks that can help.

[edit] Round numbers

The values of coins and banknotes are round numbers. The rules are:

One is a round number
Twice a round number is a round number: 2, 4, 8, 16, 32, 64
Ten times a round number is a round number: 10, 100
Half a round number is a round number: 50, 25, 12.5, 6.25
The tenth of a round number is a round number: 5, 2.5, 1.25, 1.6, 3.2, 6.4

Now 6.25 and 6.4 are approximately equal to 6.3, so we don't care. Thus the round numbers between 1 and 10 are these:

 Ratio  1    1.25 1.6  2    2.5  3.2  4    5    6.3  8   10 dB     0    1    2    3    4    5    6    7    8    9   10

This useful approximate table of logarithms is easily reconstructed or memorized.

[edit] The 4 → 6 energy rule

To one decimal place of precision, 4.x is 6.x in dB (energy).

Examples:

10 log₁₀(4.0) → 6.0 dB
10 log₁₀(4.3) → 6.3 dB
10 log₁₀(4.7) → 6.7 dB
10 log₁₀(4.9) → 6.9 dB

[edit] The "789" rule

To one decimal place of precision, x → (½ • x + 5.0 dB) for 7.0 ≤ x ≤ 10.

Examples:

10 log₁₀(7.0) → ½ • 7.0 + 5.0 dB = 3.5 + 5.0 dB = 8.5 dB
10 log₁₀(7.5) → ½ • 7.5 + 5.0 dB = 3.75 + 5.0 dB = 8.75 dB
10 log₁₀(8.2) → ½ • 8.2 + 5.0 dB = 4.1 + 5.0 dB = 9.1 dB
10 log₁₀(9.9) → ½ • 9.9 + 5.0 dB = 4.95 + 5.0 dB = 9.95 dB
10 log₁₀(10.0) → ½ • 10.0 + 5.0 dB = 5.0 + 5.0 dB = 10 dB

[edit] −3 dB ≈ ½ power

A level difference of ±3 dB is roughly double/half power (equal to a ratio of 1.995). That is why it is commonly used as a marking on sound equipment and the like.

Another common sequence is 1, 2, 5, 10, 20, 50 ... . These preferred numbers are very close to being equally spaced in terms of their logarithms. The actual values would be 1, 2.15, 4.64, 10 ... .

The conversion for decibels is often simplified to: "+3 dB means two times the power and 1.414 times the voltage", and "+6 dB means four times the power and two times the voltage ".

While this is accurate for many situations, it is not exact. As stated above, decibels are defined so that +10 dB means "ten times the power". From this, we calculate that +3 dB actually multiplies the power by 10^3/10. This is a power ratio of 1.9953 or about 0.25% different from the "times 2" power ratio that is sometimes assumed. A level difference of +6 dB is 3.9811, about 0.5% different from 4.

To contrive a more serious example, consider converting a large decibel figure into its linear ratio, for example 120 dB. The power ratio is correctly calculated as a ratio of 10¹² or one trillion. But if we use the assumption that 3 dB means "times 2", we would calculate a power ratio of 2^120/3 = 2⁴⁰ = 1.0995 × 10¹², giving a 10% error.

[edit] 6 dB per bit

In digital audio linear pulse-code modulation, the first bit (least significant bit, or LSB) produces residual quantization noise (bearing little resemblance to the source signal) and each subsequent bit offered by the system doubles the (voltage) resolution, corresponding to a 6 dB (power) ratio. So for instance, a 16-bit (linear) audio format offers 15 bits beyond the first, for a dynamic range (between quantization noise and clipping) of (15 × 6) = 90 dB, meaning that the maximum signal (see 0 dBFS, above) is 90 dB above the theoretical peak(s) of quantization noise. The negative impacts of quantization noise can be reduced by implementing dither.

[edit] dB chart

As is clear from the above description, the dB level is a logarithmic way of expressing not only power ratios, but also voltage ratios The following tables are cheat-sheets that provide values for various dB power ratios and also "voltage" ratios.

[edit] Commonly used dB values

dB level	power ratio	dB level	voltage ratio
−30 dB	1/1000 = 0.001	−30 dB	$\sqrt{1/1000}$ = 0.03162
−20 dB	1/100 = 0.01	−20 dB	$\sqrt{1/100}$ = 0.1
−10 dB	1/10 = 0.1	−10 dB	$\sqrt{1/10}$ = 0.3162
−3 dB	1/2 = 0.5 (approx.)	−3 dB	$\sqrt{1/2}$ = 0.7071
3 dB	2 (approx.)	3 dB	$\sqrt{2}$ = 1.414
10 dB	10	10 dB	$\sqrt{10}$ = 3.162
20 dB	100	20 dB	$\sqrt{100}$ = 10
30 dB	1000	30 dB	$\sqrt{1000}$ = 31.62