Collision problem
From Wikipedia, the free encyclopedia
The r-to-1 collision problem is an important theoretical problem in complexity theory, quantum computing, and computational mathematics. The collision problem most often refers to the 2-to-1 version [1]: given n even and a function  , we are promised that f is either 1-to-1 or 2-to-1. We are only allowed to make queries about the value of f(i) for any
, we are promised that f is either 1-to-1 or 2-to-1. We are only allowed to make queries about the value of f(i) for any 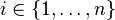 . The problem then asks how many such queries we need to make to determine with certainty whether f is 1-to-1 or 2-to-1.
. The problem then asks how many such queries we need to make to determine with certainty whether f is 1-to-1 or 2-to-1.
[edit] Classical Solution
Clearly, for the 2-to-1 version, we would need to make at most n / 2 + 1 queries to determine the answer. If the function is 2-to-1, then we know that the image of  under f must contain exactly half of the members of that set. After making n / 2 distinct queries we therefore have the entire image of f iff it is 2-to-1. The very next distinct query settles it: if we get a number that is already in our image set, then f must be 2-to-1 and if we do not, then f must be 1-to-1.
under f must contain exactly half of the members of that set. After making n / 2 distinct queries we therefore have the entire image of f iff it is 2-to-1. The very next distinct query settles it: if we get a number that is already in our image set, then f must be 2-to-1 and if we do not, then f must be 1-to-1.
More generally, if f is either r-to-1 or 1-to-1 and n is a multiple of r, then it takes n / r + 1 queries to be sure.
[edit] Quantum Solution
To be worked on...
[edit] Randomized Algorithms
Also to be worked on... should include the  result.
result.
- ^ Scott Aaronson (1994). "Limits on Efficient Computation in the Physical World" (PDF).
Category: Quantum mechanics
